自由なアーキテクチャーのNN法と学習アルゴリズム-MTC6c

2018.11.23

情報化学+教育 > MAGICIAN 養成講座 >　講義資料 > 第6c回 ニューラルネットワーク法のネットワーク構造と学習アルゴリズム

MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。

ニューラルネットワーク法のネットワーク構造を自由に設計してみましょう。

結果を定量的に扱いたい場合には、NNは3層型のニューラルネットワークを用いる事が多いようです。
１層目は入力層、2層目は中間層、3層目は出力層と呼びます。しかし、3層型で扱わなければならないという決まりはありません。
最近流行りのディープ・ラーニングでは、この中間層の数が非常にたくさんになっています。

筆者は部分4層化NNなども検討してきました。

また、学習のアルゴリズムは、多くの場合、誤差逆伝播法が使われます。
これは、ニューラルネットワークの荷重行列を、教師データと計算値の誤差が一番小さくなるように動かしていきます。

この誤差逆伝播法は、非常に強力で、複雑な化学の現象にも追随できたので、20年前のブームに繋がりもしましたが、逆に廃れる原因にもなりました。

しかし、ネットワーク構造も学習アルゴリズムも、教科書に書いてある通りにしなければならないわけではありません。
数学的な根拠は置いておいて、化学に合わせたモデルを作成してみましょう。

準備

　第6a回のニューラルネットワーク法の基礎で説明したように、非線形であるSin曲線をニューラルネットワークに学習させる際には、ある関数を仮定して、その関数の係数を求めます。

f(y)=A1* / [1+exp(-(B1*X1+B2*1))＋
　　A2* / [1+exp(-(B3*X1+B4*1))＋
　　A3* / [1+exp(-(B5*X1+B6*1))

という曲線を仮定して、誤差が最小になるA1-A3, B1-B6の組を見つければ良いだけです。

A1= -2.14 B1= -1.84 B2= 0.30
A2= -1.01 B3= 0.04 B4= 0.31
A3= 2.11 B5= -1.87 B6= 1.57

のように置くと、下図に示すように良好にSinカーブを再現できます。

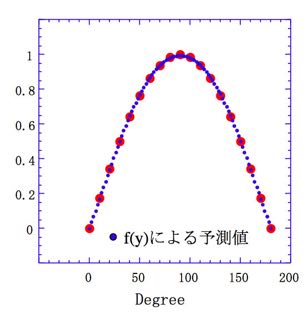
ここで、大事なのは、「曲線としてどんな曲線を仮定するは各人の自由である」という点です。第6a回でも述べたように、次の関数でも良好にSin曲線を再現できます。

f(y)=A1*(1/X1)+A2*log(X1)+A3*(X^2 )+A4*(sqrt(X1)) +Const.

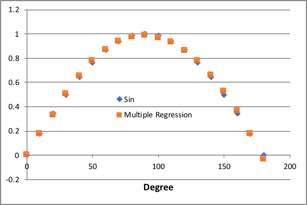
A1:-0.0295014488567471
A2:-1.39531945518547
A3:-0.000099576191739178
A4:0.464330591108506
Const.：0.113247988857779

これらの係数は収束計算を行わなくても、重回帰法で簡単に求まります。
問題は、X1=0の時の値が求まらないだけです。

ニューラルネットワーク法で、

f(y)=1* / [1+exp(-y)]

というシグモイド関数を用いている理由は、生物の刺激-応答曲線に似ているからとかいう、とってつけたような説明があります。

実はそれには余り意味がないと私は思っています。
単にシグモイド関数の微分が

f(y)’=(1-f(y))*f(y)

と元のf(y)で表す事ができる為、誤差逆伝播法(EBP: Error Back Propagation)で機械学習させる際に都合が良い（どちらに、どれだけ動かせば誤差がどれだけ小さくなるか理解しやすい）からだと思います。

化学の物性値はもともと誤差を含んでいたり曖昧であったりする事が多いです。

例えば、ある物質の水への溶解度は、水100gに対する溶解度(g)で表すことが多いです。
その際に、よく水に溶ける化合物は、100g(溶質)/100g(水)以上は測定せず、logS=2.0としてしまう事があります。

様々なデータ値で、logS >2.0、引火点 >110℃、屈折率 <1.2などの表記は書籍では当たり前に存在しました。

ところが、デジタルのデータベースは、フィールド値の属性は事前に決めて置く必要があります。
”>2.0”はテキスト属性であり、数値属性ではない為、DBに入力できなくなります。そのうちに、不等号は消えてしまって数値だけが一人歩きを始める例が散見されます。

また、測定限界の問題もあります。昔であれば水への溶解度は、1mgが測定限界であったでしょう。しかし、今日の測定装置ではもう3桁低くても測定できたりします。
全ての化合物について最新のデータが揃えば良いのですが、logS が, -4ぐらいのものと-7ぐらいのものが、測定方法の新旧によって混在してしまう可能性があります。

そうした誤差や曖昧さを含んだ値を誤差逆伝播法で機械学習させると、必要以上に中間層のニューロンを増やさないと収束しなくなります。

その結果として予測性能が非常に劣るニューラルネットワーク・システムができあがるなどの問題が生じます。

それを回避する一つのやり方は、フィードフォワードの学習法を使うことです。
誤差を微分係数によって逆伝播させないので、シグモイド関数を使う必要もありません。係数の決定には第7回で説明した遺伝的アルゴリズムを使います。

そうしたやり方で、ネットワーク構造も学習アルゴリズムも自由に設計できることを今回の講座で示しましょう。

新規アーキテクチャーNN法

非線形動作関数が自由で良いなら、どのような関数が良いでしょうか？

Log, 三角関数、べき乗など様々な非線形関数がありますが、私の選んだのはPower関数です。
化学工学の領域ではよく使われます。
例えばスタントン数という無次元数は次式で表す事ができます。

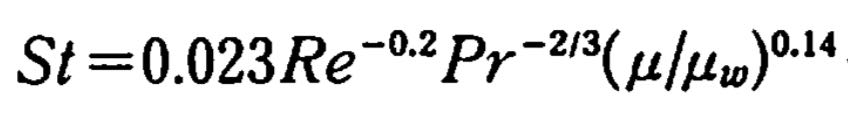
このような指数の係数を求めるには、両辺のlogをとって重回帰を計算すれば良いです。

さらに複雑になった時には、遺伝的アルゴリズム(GA)を用いて係数を求めます。

例えばイオン液体の物性値を求めるニューラルネットワークを考えてみましょう。
イオン液体の物性値は、アニオンの種類とカチオンの種類で決まります。

アニオンの種類はあまり多くありませんがカチオンの種類は非常に多くあります。
カチオンの構成としては、主骨格（イミダゾールなど）に対して側鎖の長さや種類を色々変えたものが開発されています。

この様々なイオン液体を特徴付ける識別子として、半経験的分子軌道計算法、MOPAC、PM3の計算結果なども用います。
この結果は Physical chemiatry C に投稿しました(Estimation of Ionic Conductivity and Viscosity of Ionic Liquids Using a QSPR Model)。

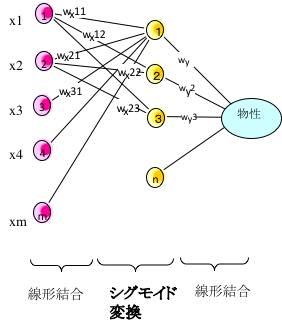
今回用いたNNのアーキテクチャーを模式図で表すと以下のようになります。

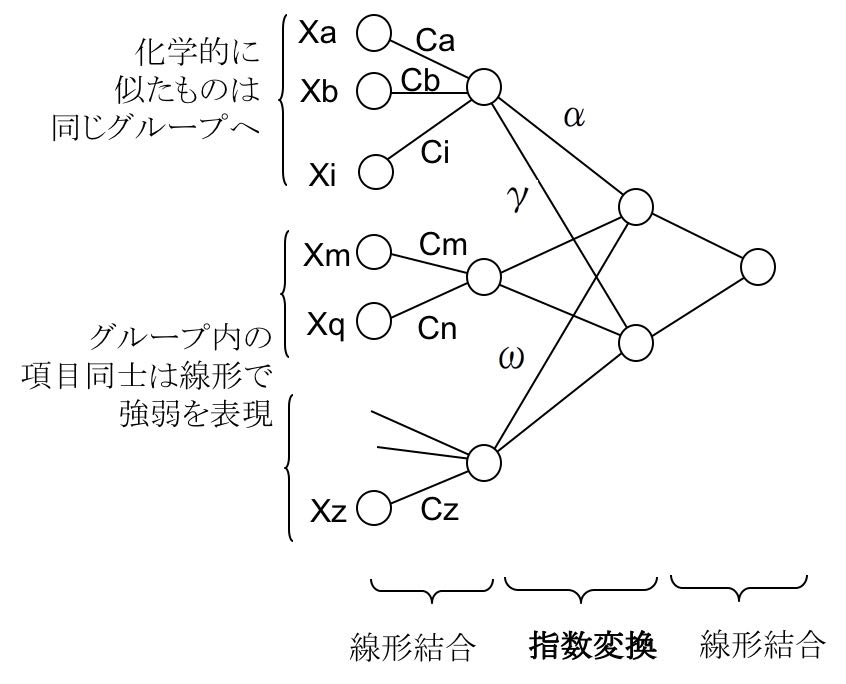
P= C0 + Σ[(Ca*Xa+Cb*Xb・・Ci*Xi+1)^α
　・・・
　*(Cm*Xm+・・・ +Cq*Xq+1)^γ　
　・・・
　*(・・・　 　　+Cz*Xz+1)^ω ]

で物性値が表現できるとして、各係数を、遺伝的アルゴリズム(GA)を用いて求めました。

ここで重要なのは、化学的に似たものは同じグループに入れる事です。

通常のニューラルネットワーク法では、入力された値は、中間層ニューロンで強弱の差はあっても全て結合しています。再構築学習法を取り入れて影響の少ない結合荷重をゼロにしても、冗長性は残ってしまいます。

この新しいアーキテクチャーでは、グループ内は線型結合で、グループ間は指数変換したのちに掛け算で表現されます。
化学者が化学の知識を総動員してグループを設計するのが大事なポイントになります。

このニューラルネットワーク法をMIRAI法と命名しました。

例えばイオン液体の密度の推算式を構築してみましょう。
新しいアーキテクチャーでは、次のように求まる。

0.1772+1.2537*(
POWER((Temp.*-0.0008656+1),0.563)*
POWER((TFSI*0.905+Br*0.413+Cl*-0.0887+PF6*0.6445+BF4*0.176+CF3SO3*0.441+1),0.418)*
POWER((Am4*-0.290+PRL*0.468+PZ*-0.490+IMD*-0.368+PRZ*-0.351+1),-0.0463)*
POWER((R1*-0.0191+R2*-0.00337+R3*-0.0195+R4*-0.00123+1),1.395)) Scheme(1)

グループとしては、温度項、アニオン項、カチオン項、側鎖の長さの４グループとします。カチオン項の指数は-0.0463と非常に小さいので、密度にはほとんど影響を与えません。（Am4:４級アミン、PRL: Pyrol, PZ: Pyridine, IMD: Imidazole, PRZ: Pyrazole）
R１からR４は窒素につくアルキル基の炭素長さを入力します。TFSIは(CF3SO2)2N- という構造のアニオンです。

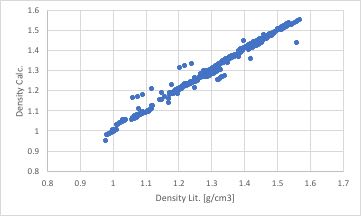
Scheme(1)によって計算された密度を実験値に対してプロットすると下図のようになります。

図中、ほとんどのデータポイントは綺麗に直線の上に乗りますが、７点ほど並行に上にずれたデータポイントが存在します。

その化合物がどのような構造かを確認すると、３置換のイミダゾール化合物である事がわかりました。

このような結果が得られる事がフィード・フォワード型のニューラルネットワーク法を使う事の大きなメリットです。カチオンのグループの中に3IMDを定義する必要がある事がわかります。

３置換イミダゾール

同じデータを用いて再構築ニューラルネットワーク法で予測式を構築してみます。

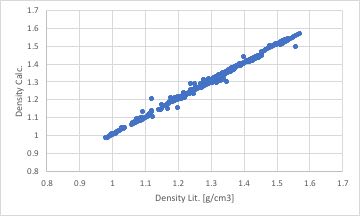
誤差逆伝播型のニューラルネットワーク法を用いると、教師データが正しいとして、教師データとNNの計算値の差分が小さくなるように結合荷重行列を調整します。そこで、３級イミダゾールを定義し直さなくても良好に収束してしまいます。

論文とかに記載するのであれば、相関係数が高い後者のモデルを採用したほうが見栄えは良くなります。しかし、後者のモデルでは予測性能は劣る事になります。

化学の領域では、こうした識別子が十分ではない場合がある事、教師データと言えども、誤差やエラーを含んでいることもある事から、フィード・フォワード型のNN法と比較検証するのは大事な事です。

識別子の抽象化

このような方法で、３置換のイミダゾールを識別子として加えるという方法をとっていくと、カチオンの種類がどんどん増えていきます。
　
それにしても、実測値があって式に組み込むまでは新しいカチオンの予測は不可能になります。

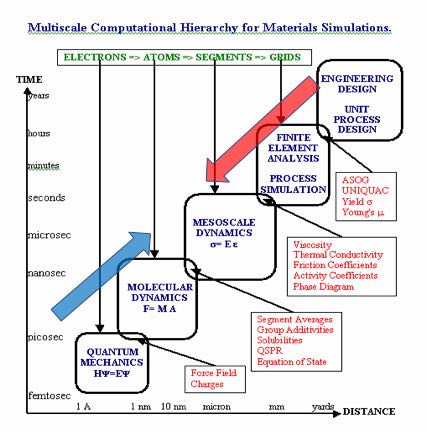
その時役に立つのが、第１回でも使った次の図です。
分子軌道法や分子動力学法は演繹法で原子を足したら分子、分子を足したら物質と左下から右上に青い矢印の方向で考えていきます。
帰納法はこのカチオンの性能はこう、あのカチオンの性能はこう、側鎖を外してと、右上から左下に考えていきます。

そして、新しいカチオンの性能を予測したくなった時には、足りないパラメータは他の手法を借用しようと考えます。

マテリアルズ インフォマティクス(MI)のインフォマティクスとは情報学のことです。情報ソースは何を使ってもよいのです。
実験値、分析値、理論値など様々な情報を組み合わせて答えを探していきます。

よく使うのが、分子軌道法の計算結果です。電荷, HOMO, LUMO, ダイポール・モーメントなどは簡単に得られます。

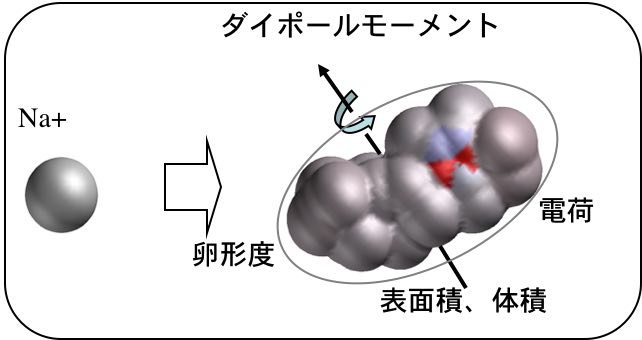
また、分子表面積、分子体積、卵形度なども計算できます。

NaClのような塩は融点が何千度にもなる。それに対してイオン液体の多くは室温で液体になります。
その違いを見ながら、カチオンの種類を識別子に使うのではなく、もっと抽象化したカチオンを表す指標を考えていきます。

この例では、イオン液体の粘度を推算する式を、カチオンの部分をMO計算結果などと置き換えて作ってみましょう。

Log(Vis)=0.112+1.022*(
POWER((温度*0.00344+1),-3.649) *
POWER((ダイポールモーメント*1.130+1),0.131)*
POWER((LUMO効果) *
POWER((分子表面積*0.841+1),0.138)*
POWER((Ovality*0.837+1),-1.044)*
POWER((窒素電荷効果)*
POWER(アニオン効果) scheme(2)

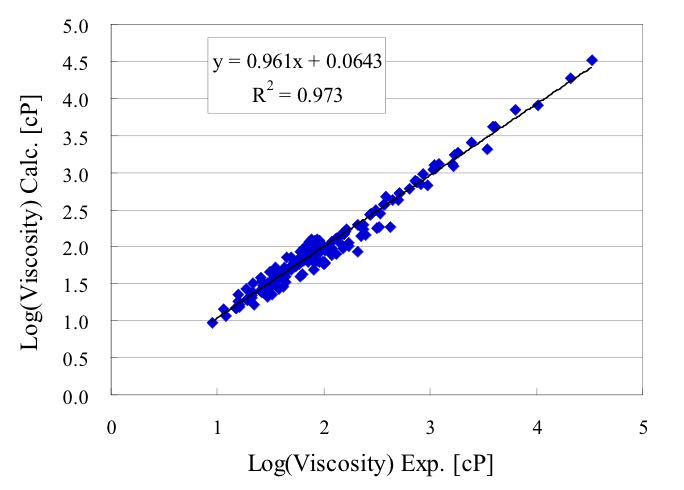
カチオンの種類の代わりに、ダイポールモーメント、LUMO, 分子表面積、卵形度、窒素電荷を使うことによって上図の結果が得られました。

式を構築するのに使わなかったデータを用いて予測性能を検証すると下図のようになりました。

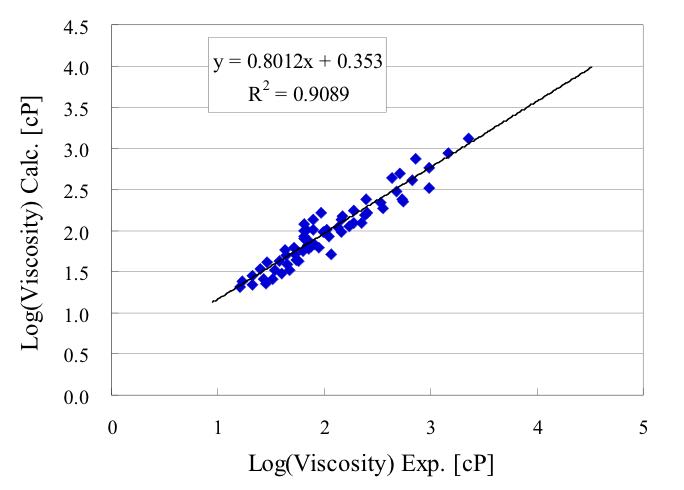
Scheme(2)が得られると、各項目の効果を取り出して検証する事ができるようになります。

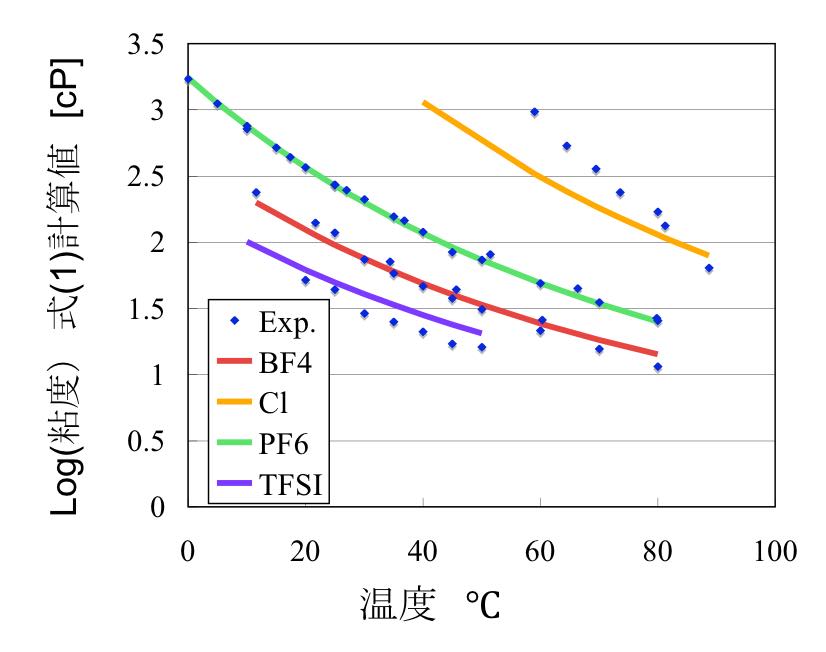
例えばアニオンを変化させたときの粘度の温度依存性はscheme(2)から、下図のように求まります。

このように、POWER((温度*0.00344+1),-3.649)とPOWER(アニオン効果)を切り出してくれば簡単に検証できます。
通常のニューラルネットワークでは、ネットワークの中身はブラックボックスになってしまうので、このような検証を行うのは楽ではありません。

この新しいアーキテクチャーのニューラルネットワークでは、グループ内の各項目の係数は線形結合で表してあります。

例えば、アニオンの効果は下式になります。

POWER((TFSI*0.321+Br*2.787+Cl*3.196+PF6*1.302+BF4*0.681+
CF3SO3*0.513+CF3COO*0.497+CH3COO*1.602+CF3BF3*0.374+
C2F5BF3*0.206+MeOSO3*0.990+1),0.6840723)

この係数が小さいものは粘度が低くなることは式から明らかでしょう。ClやBrのような単原子では粘度は大きくなってしまい、TFSIなどでは粘度が低下します。その原因を明らかにするために、ここで得られた係数とアニオンの体積をプロットしてみました。

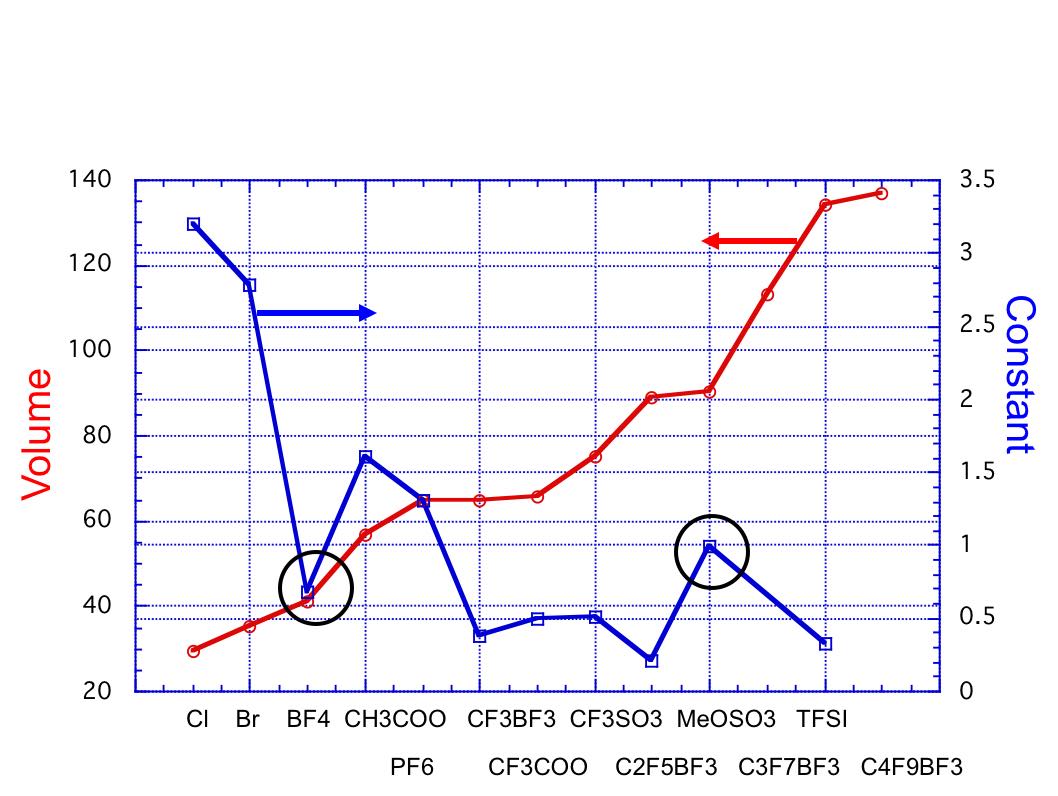
上図に示すように、基本的にはアニオンが大きくなるにつれ、係数は小さくなる事がわかります。例外はBF4とMeOSO3です。体積だけでは説明が不十分な理由の一つはダイポールモーメントの効果でしょう。

アニオンではなくカチオンの部分についてではありますが、この効果は次式で表されます。

POWER((ダイポールモーメント*1.130+1),0.131)

MOPACで計算されたダイポールモーメントに対して、このダイポールモーメントの効果を評価すると下図のようになります。
つまり同じ分子の大きさであっても、分子の中心から電荷の位置がずれてダイポールモーメントが大きくなると、粘度は下がる事がわかります。

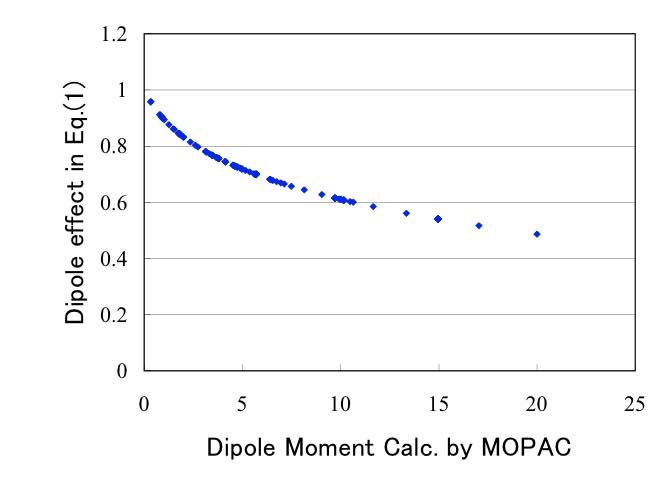
また、卵形度（球に近づくほど１に近くなる）の効果は次式で表されます。

POWER((Ovality*0.837+1),-1.044)

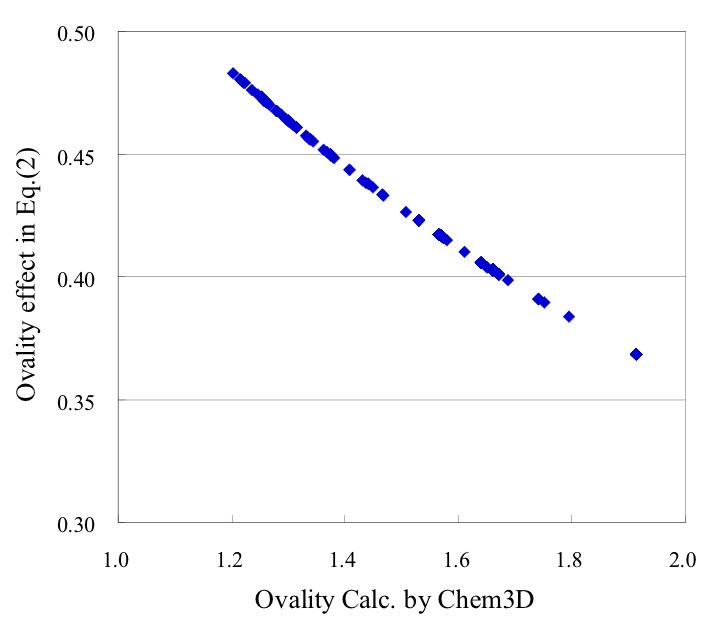
球からずれるにつれ急に粘度が下がる事がわかります。
NaClでは、アニオン、カチオンの両方が完全球形となるので融点が非常に高くなるのでしょう。

このような推算式が得られると、任意の温度での密度と粘度の計算値が得られます。すると任意の温度での動粘度(粘度／密度)が得られるので、潤滑油の分野で重要な粘度指数を簡単に計算で出す事ができます。
100℃と40℃で粘度差が小さいイオン液体は側鎖の長さが短いなどの特徴が計算するだけで得る事ができます。

以上のように、ここで設計した新しいアーキテクチャーのNNは、フィードフォワード法を用いているので、教師データのエラーや誤差に強くなります。また、ニューロン同士の結合が制限されているので、情報の流れが明瞭にわかるという特徴を持っています。

雑感

　このアーキテクチャーを持つニューラルネットワーク法は、2005年頃に開発したものです。非線形関数として指数関数とガウス関数などを選べたり、多項式を1つ以上足し合わせる、グループ間を掛け算ではなく足し算で表現できるなどの機能を搭載したJavaのアプリケーションです。（マシンを問わずに動作させる事ができます。）

実際問題としてイオン液体の物性値を収録してみると同じ構成でも物性値が大きく異なる例にでくわします。

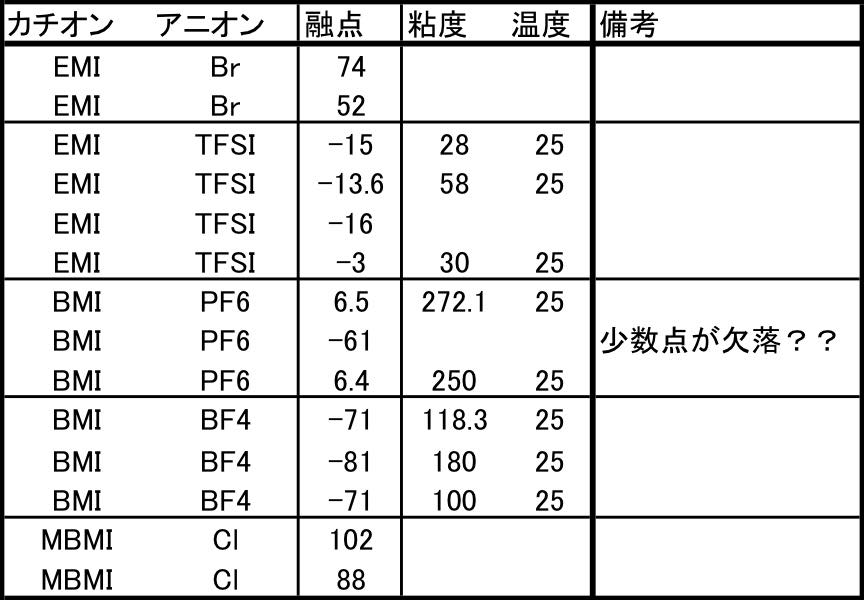
全く同じ構成なら、こうしたデータは収束しないので見つけるのは楽です。しかし、微妙に測定温度異なっていたりするとデータのクレンジングは非常に難しくなります。

そうした時にフィードフォワード型の学習法は有効です。

問題は、学習時間でした。
遺伝的アルゴリズム法はあるところまでの収束は速いです。
しかし、そこを過ぎると突然変異と交叉操作だけでは中々十分には収束していきません。

ある多峰性の山があった時に、収束速度を早めるために集中的に遺伝子をその領域に投入したらどうか？　しかし、そこが実はローカル・マキシマムであって、グローバル・マキシマムでなかったらどうなるか？　など、色々な問題があります。そうした時、数学の問題ではなく楽しく考える事ができ、簡単に実装できのがGA法の良いところです。

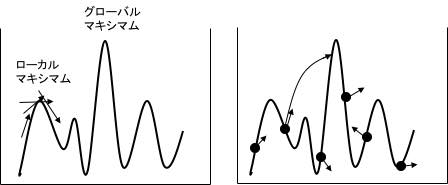
例えば、働きアリは常に10%のアリは働かないで遊んでいるそうです。その10%のアリを取り除いてしまうと、また10%のアリは働かないで遊び始める。標高が高そうな部分が見つかったら９割の遺伝子はそこに投入するけど、１割は他の探索空間を遊ばせる、アリ型学習法とかを自由に設計して試す事ができます。

それにしてもコンピュータのスピードはこの15年間で飛躍的に早くなりました。今回再計算を試してみて心底そう思いました。そうなってくると、今まで計算が遅くなるので、外していた機能を復活させようかと思います。

通常の研究では、化学者に求められているのは、識別子を考える事ぐらいでしょう。機械学習のアルゴリズムやツール作成までは求められていません。
しかし、化学の原理原則を理解している「化学者ならではの、学習アルゴリズムを考える」のは化学者にしかできないのでは無いでしょうか。

ある現象を詳しく見てきた者であれば、頭の中にある程度のスキームが出来上がっているはずです。それをブラックボックスのNNに譲り渡す必要はありません。少しだけプログラムの書き方を学ぶだけで試す事ができます。

情報化学+教育 > MAGICIAN 養成講座 >　講義資料 > 第6c回 ニューラルネットワーク法のネットワーク構造と学習アルゴリズム

Copyright pirika.com since 1999- 
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。