2025.2.5
情報化学+教育 > YMB Pro for MI >
注意:HSPiPに搭載の機能ではありません
カーボンナノチューブとポリマーの適合性を調べている論文を読んだ。

ウレタンゴムに混ぜ込んで、導電性のゴムを作りたいらしい。臨界界面張力で評価し、ある値以上で抵抗が高くなる領域があるという。CNTがよく分散しすぎてCNT同士の接触が悪くなった結果という。(材料の強度アップであれば逆によく分散したほうが良い?)
車両用炭素材料 (MAGICIAN資料)2018.11.27
このテーマは昔からよく取り扱った。今回は最先端の方法を使う。
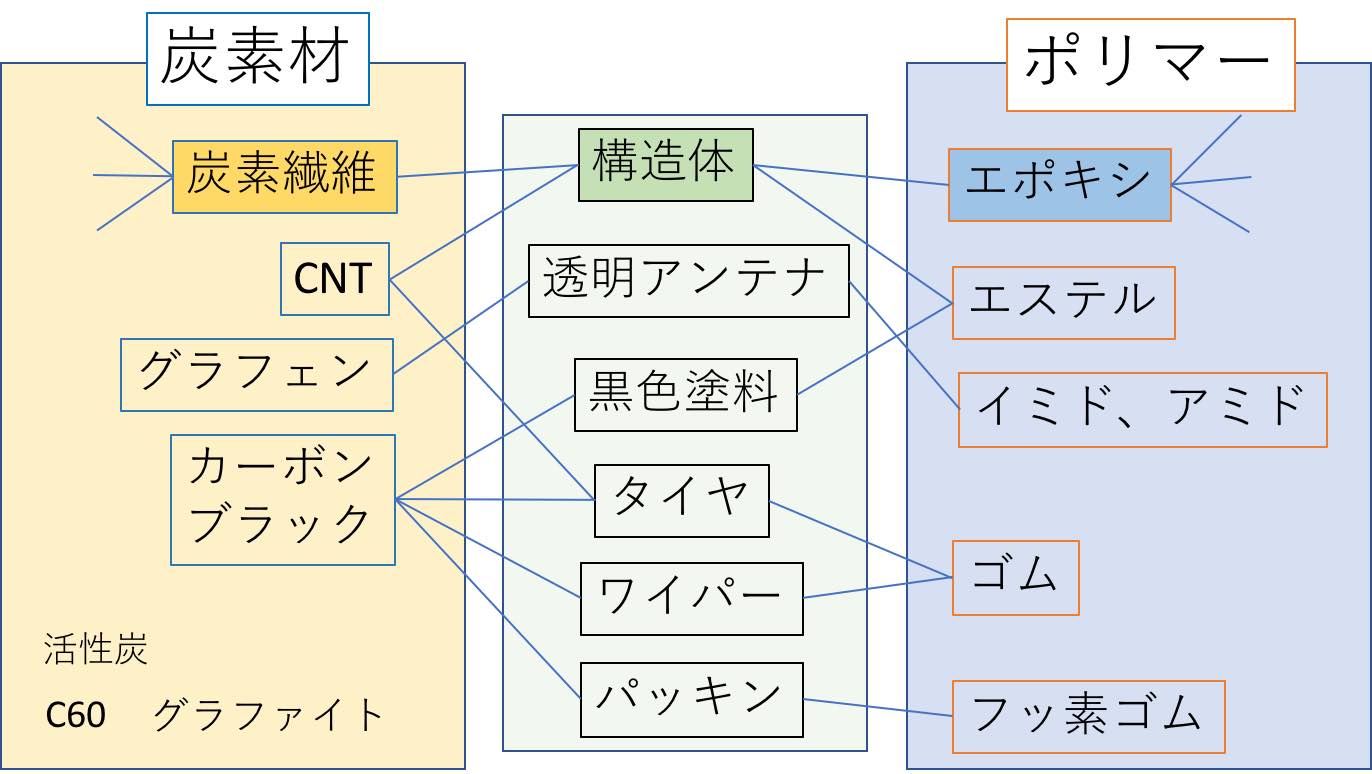
2015年の大学の授業でも取り上げた。
次世代HSP2で考える炭素材料の複合化
切り口を変えて、YMB25Pro4MIを使った複合化を考えて行こう。
接着とSP値 2010.10.2
かなり昔に書いたように、接着にはHSPが関与しているという解釈はありうる。
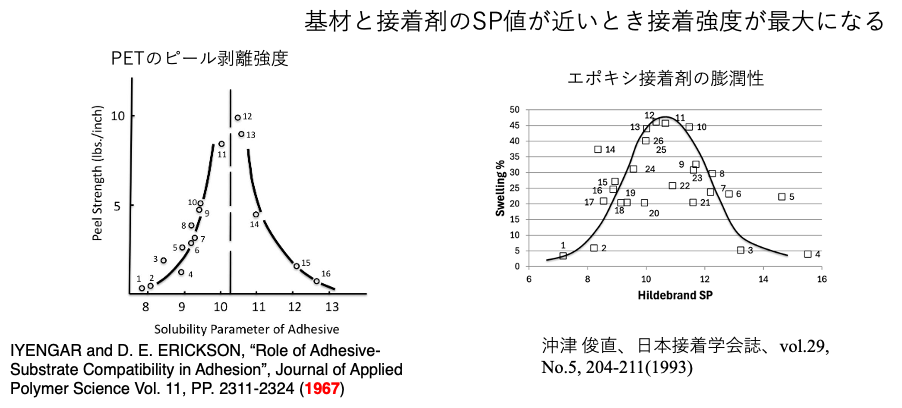
臨界表面張力と接着
しかし、同じように臨界表面張力が近い材料はよく接着するという解釈もある。
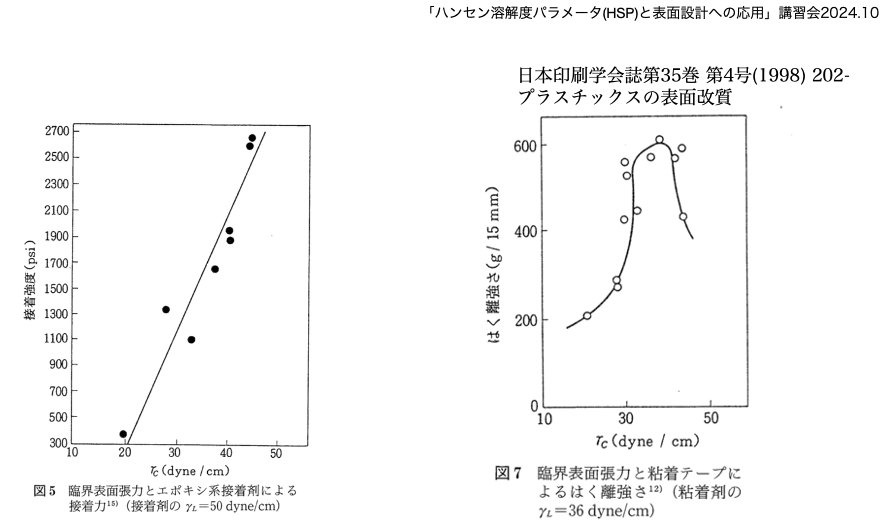
ある意味、どちらも親戚みたいなものなので、どう解釈しようが自由だ。
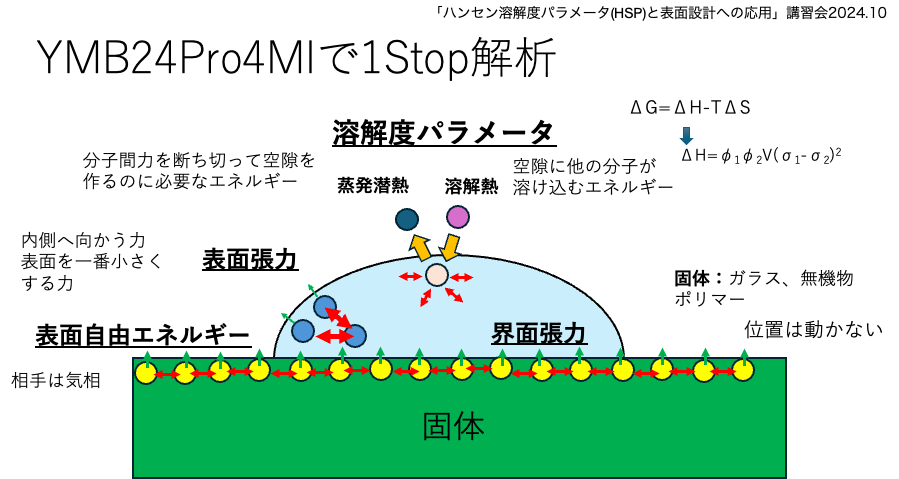
YMB25Pro4MIを持っていると1Stopでどちらも計算できるのでやってみよう。
HSPを使った評価方法 (Sphere法の基本)
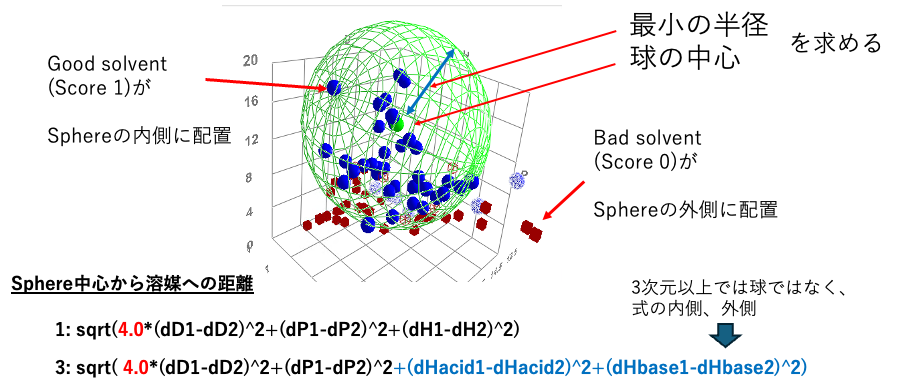
Sphere法というのはHansen先生が作られた、溶質のハンセンの溶解度パラメータ(HSP)を探索するアルゴリズムだ
HSPが既知の溶媒を(dD, dP, dHをベクトルとみなして)3次元空間にプロットする。良溶媒を青く塗る。貧溶媒を赤く塗る。良溶媒と貧溶媒の境界は研究者が定めて良い。この溶媒がプロットされた空間をハンセン空間と呼ぶ。すると、青い良溶媒はハンセン空間上で集まって球(Sphere)を作っていることにハンセン先生が気がついた。この緑の大きなメッシュの球をハンセンの溶解球と呼ぶ。そして溶解球の半径を相互作用半径と呼ぶ。溶解球の中心(塗りつぶしの小さな緑の球)を溶質のHSPと定める。
dD項の分割
2017年に私の作った拡張で、dD項を分割した。これを考慮に入れないと、PTFEが接着しにくいことの説明がつかなくなる。
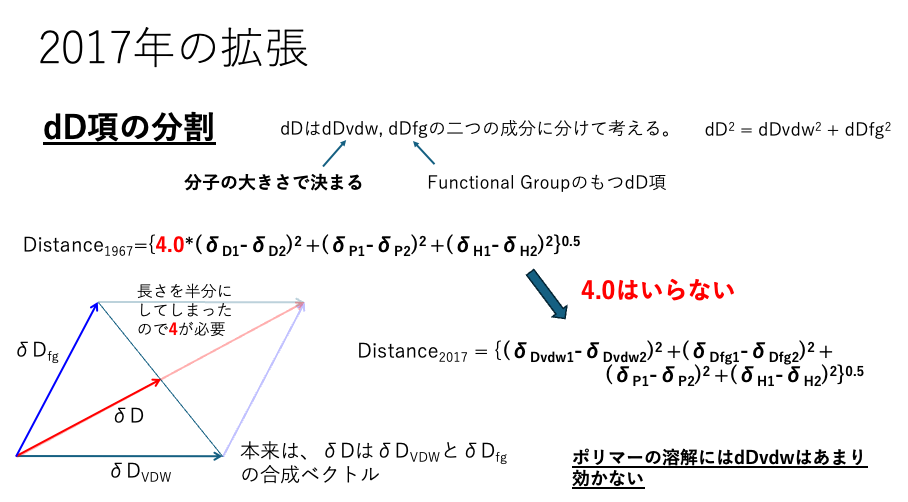
分子が大きさを持つだけで持ってしまうdDvwdと官能基によって異なる値になるdDfgの混合ベクトルを考える。(フッ素置換基はdDfgがゼロになる)
dH項の分割
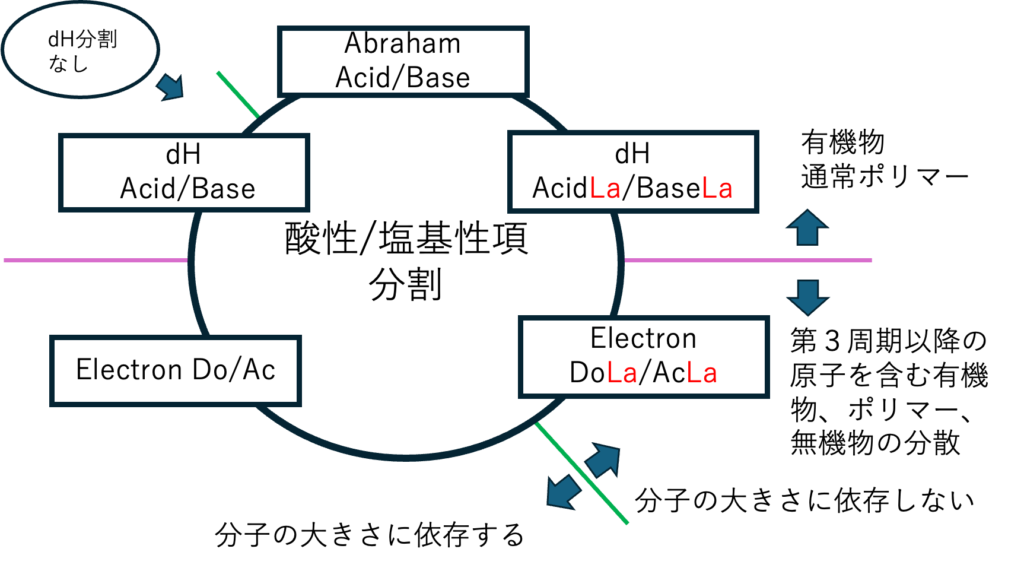
ブレンステッド酸・塩基なのかルイス酸・塩基なのか、分子中で一番大きい(La)ものだけが働いているのか検討をする。
33式を皆んな計算してしまう

HSPを使った評価

固体と固体の実績は少し少ないかもしれない。
臨界界面張力を使った評価方法
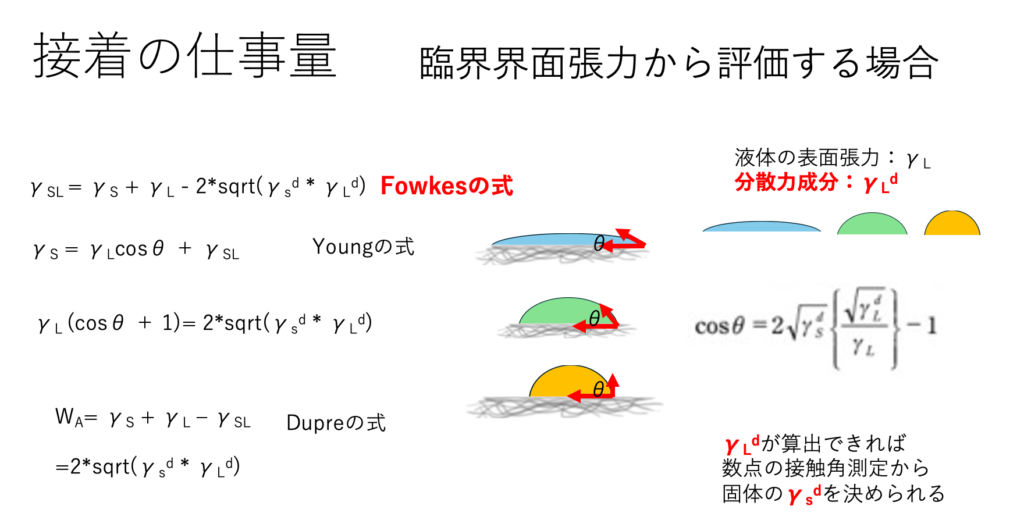
Fowkesの式をYoungの式に入れれば
γL (cosθ + 1)= 2*sqrt(γsd * γLd)となる。
液体の表面張力の分散項( γLd)がわかれば、数点の接触角の実験値からγsdを定めることができる。表面張力の分散項を求める式はいくつか提案されている。
HSP-MIRAI法による溶媒の表面張力分割式
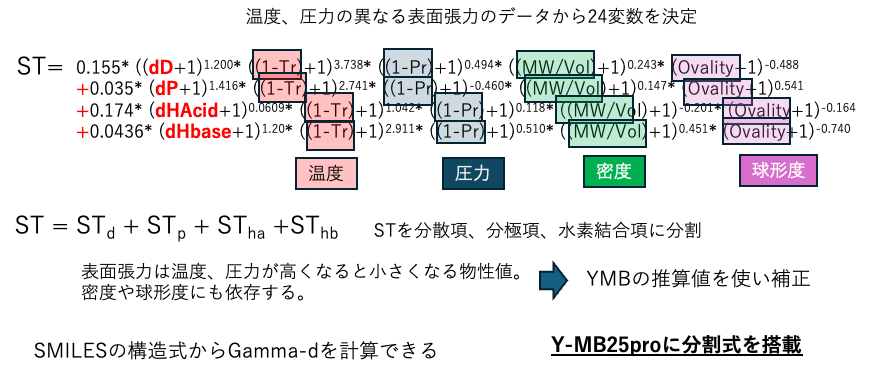
山本法は「ハンセン溶解度パラメータ(HSP)と表面設計への応用」講習会2024.10で発表している。分割式の式の形状を先に決め、温度や圧力の異なる表面張力のデータ5000ぐらいから24パラメータを決定した。任意の温度、圧力での表面張力の分散項はSMILESの分子構造があれば求めることができる。
HSP-MIRAI法によるポリマーγcの分割
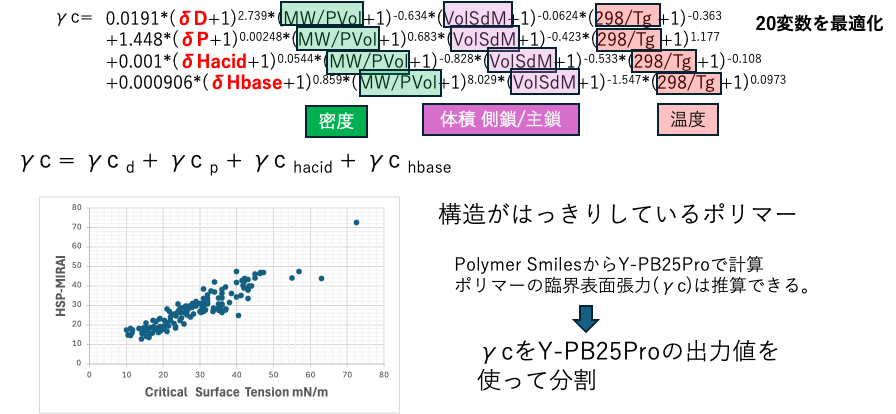
同じく、構造のはっきり解っているポリマーの臨界表面張力の分割式も作成した。これもPolymer SmilesがあればY-PB25Proで計算できる。
HSPだけしか分からないポリマー
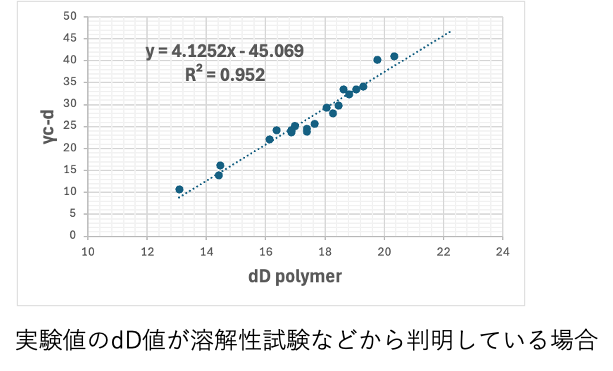
構造はわからないが、溶解性試験を行った場合には実験値のHSPが手に入っていることがある。その場合にはこの変換式からγCdを計算して使えば良い。
各論

グラフェンとポリマーの適合性
電子移動が室温で15,000 cm2/Vsとシリコンの100倍以上。銀よりも高い7.5*107 S/mの導電率、108 A/cm2以上の高電流密度耐性。もっとも強靭で、最も導電性に優れる材料である。
フラーレン(C60)とポリマーの適合性
フラーレンは1分子中に6個の電子を溜め込む電子受容性を持つ。n-型の有機半導体特性を持ち、〜1 cm2/Vs程度の電子移動度を示す。
CNTとポリマーの適合性
p型半導体的な特性、銅の1,000倍以上の高電流密度耐性、銅の10倍の熱伝導性を持つ。
こうした炭素素材は単独での利用は難しいかもしれない。HSP, 臨界界面張力からどんなポリマーと相性が良いか考えてみよう。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください
