2013.4.17
化学工学トップページ >
無次元数の推算
無次元数は、無次元量、あるいは無名数は、次元のない数量のこと(WikiPedia)。
簡単に言ってしまえば、単位のない数字のことだ。
そこで、同じ単位を持つ物性値の比は無次元になる。
例えば、臨界温度(Tc)/沸点(Bp)は無次元数になる。
何故、このような無次元数を使うのかというと、一つには物事の本質がつかめるからだ。
例えば、Tc/Bpはおおまかには1.5になることを臨界定数の推算の所で示した。
世の中には様々な液体があるが、ざっくりとはTc/Bpは1.5になって、さらに分子が小さいものは1.5が更に大きく、分子が大きいものは小さくなるという知識が得られる。
もう一つには、化学工学ではフラスコレベルから工場でのプラントまで、スケールが非常に大きく変化する。
最近ではマイクロリアクター(インクジェット技術も含む)などフラスコよりもずーっと小さい領域にまで達している。
そうしたときに、例えば流れ場の状態を考えた時に、流体の速度が km/hr, μm/s なのか単位が変わった時に状態が変わる数値で整理しているととんでもなく大変な事になる。
そうした時に無次元数であるレイノルズ数を使うと工場の配管からマイクロリアクターまで同一に扱えるので非常に便利である。
Pirikaでは化学工学上重要な物性値単独の推算方法は物性化学のページで紹介している。これらを使って無次元数を推算してみよう。
化学工学上重要な無次元数は次のものだろう。
レイノルズ数 (WikiPedia) :
代表長さ [長さの次元]、代表速度 [速さ = 長さ / 時間の次元]、動粘性係数 [長さ * 長さ / 時間の次元] の値を用いて求められ、流れ場の状態を表す無次元数となる。
形は同じで大きさが異なる物体回りの流れを比較する際、両者のレイノルズ数が同じであれば、物体回りの流体の流れは相似となりサイズは異なっても本質的には同じ現象と考えることができる。(プログラムは構築中)
プラントル数 (WikiPedia) :
動粘度と温度拡散率の比である。(プログラムは構築中)
ヌセルト数 (WikiPedia) :
伝熱の分野で、対流による熱伝達と流体(静止している流体)の熱伝導の比率を示す。対流が生じていなければ Nu = 1 である。(プログラムは構築中)
マランゴニ数 (環境工学研究所資料):
マランゴニ数は2つの流体が接した界面で起こる表面張力の局所的な不均一によって生じるマランゴニ対流を支配する無次元数。
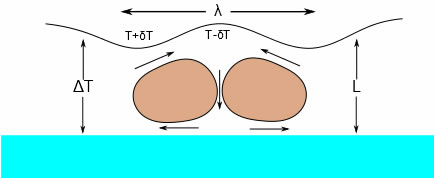
マランゴニ数の推算はインクジェットの液滴の乾燥などの分野で非常に重要になってきており、海外の研究者から推算できないか問い合わせを多く頂いている。
YouTubeの映像、インクジェット着滴後の乾燥&コーヒーステイン現象を見て頂きたい。
コーヒーステインというのは、コーヒーの液滴が乾く時に、中央部よりも周辺部にコーヒーの濃い模様が現れる現象のことだ。
これはマランゴニ対流で説明される。
日本語でマランゴニ数、マランゴニ対流と検索すると宇宙での実験ばかりが引っかかってくる。
これは無重力下では、液体は表面張力によって球形を保ったまま浮遊する。
その液滴表面の対流を検討した例なのだろう。
しかし、インクジェットなどのナノ・オーダーの現象であれば地上でもマランゴニ対流が興味深い現象に関わってくる事がわかってきた。
そこで分子の構造のみからマランゴニ数を推算するプログラムをHTML5とJavaScriptを使って作成した。次のページで試してみて欲しい。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
