2011.4.20
化学工学トップページ >
まず最初に蒸気圧のデータを準備します。
| No | P(mmHg) | T(℃) |
| 1 | 15.1 | 17.4 |
| 2 | 32.8 | 30 |
| 3 | 59.0 | 40 |
| 4 | 59.0 | 40 |
| 5 | 95.5 | 50 |
| 6 | 152.8 | 60.1 |
| 7 | 277.2 | 74.9 |
| 8 | 404.3 | 75.2 |
| 9 | 670.6 | 100 |
圧力単位は、mmHgかKPa、温度は°CかKで表計算ソフトなどを使いテーブルを作ってください。
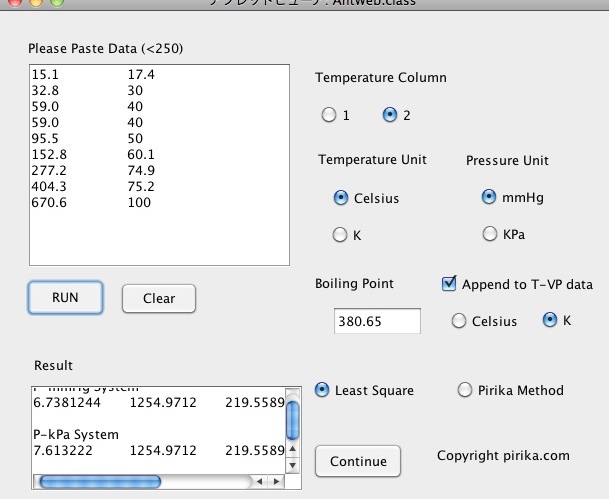
次にソフトウエアーを立ち上げます。環境によって見栄えは異なりますが、下のようなスタート画面が現れます。(画面はHTML5のバージョン)
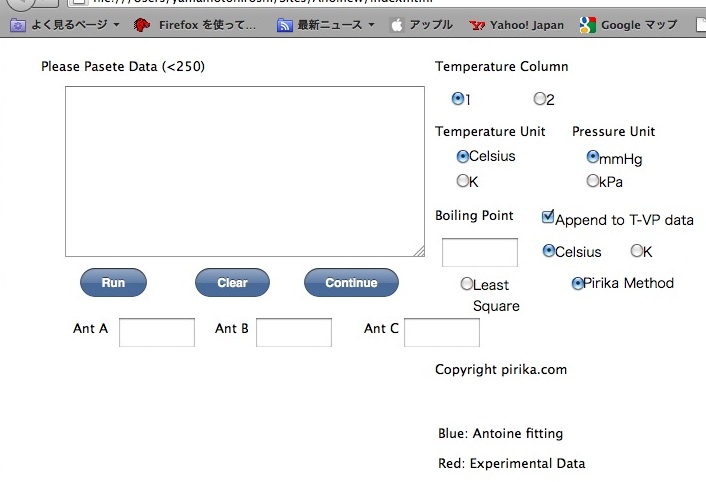
- 左上のテキストエリアに先ほど準備した蒸気圧データの中身だけペーストします。
(データの区切りはTabになります。最大データ数は250です。) - 2列のうち、どちらが温度の列なのかを指定します。
- 温度と圧力の単位を指定します。
- 次に沸点の値とその単位を入れます。
このプログラムは、Antoine BとCパラメータの初期値に沸点を使いますので、沸点は必須です。
沸点のデータ(760mmHg)を蒸気圧データに含める場合にはAppend to T-VP dataにチェックを入れてください。
蒸気圧データにすでに含まれる場合にはチェックをはずしてください。
そして、RUNボタンを押します。
すぐに結果とグラフが現れます。
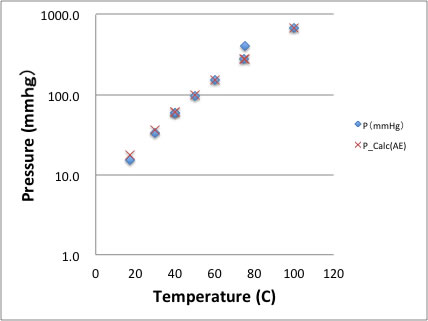
赤丸が実験のデータ。
青丸がフィッティングしたAntoine式で計算したデータです。
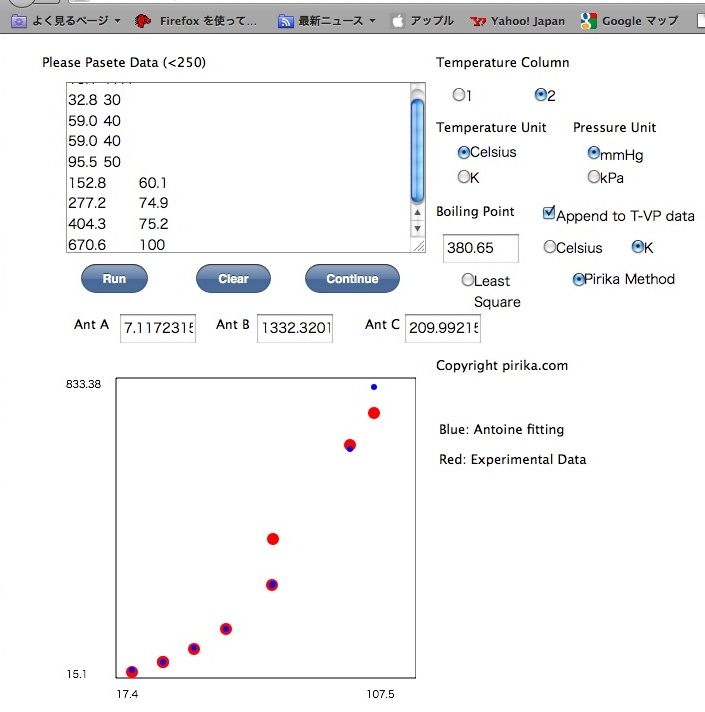
結果をコピーして元の表計算に貼り付けます。
そして蒸気圧を計算して実験値との差を見ます。
下のテーブルはプログラムのオプションとしてAE(PirikaMethod)を選択したものです。
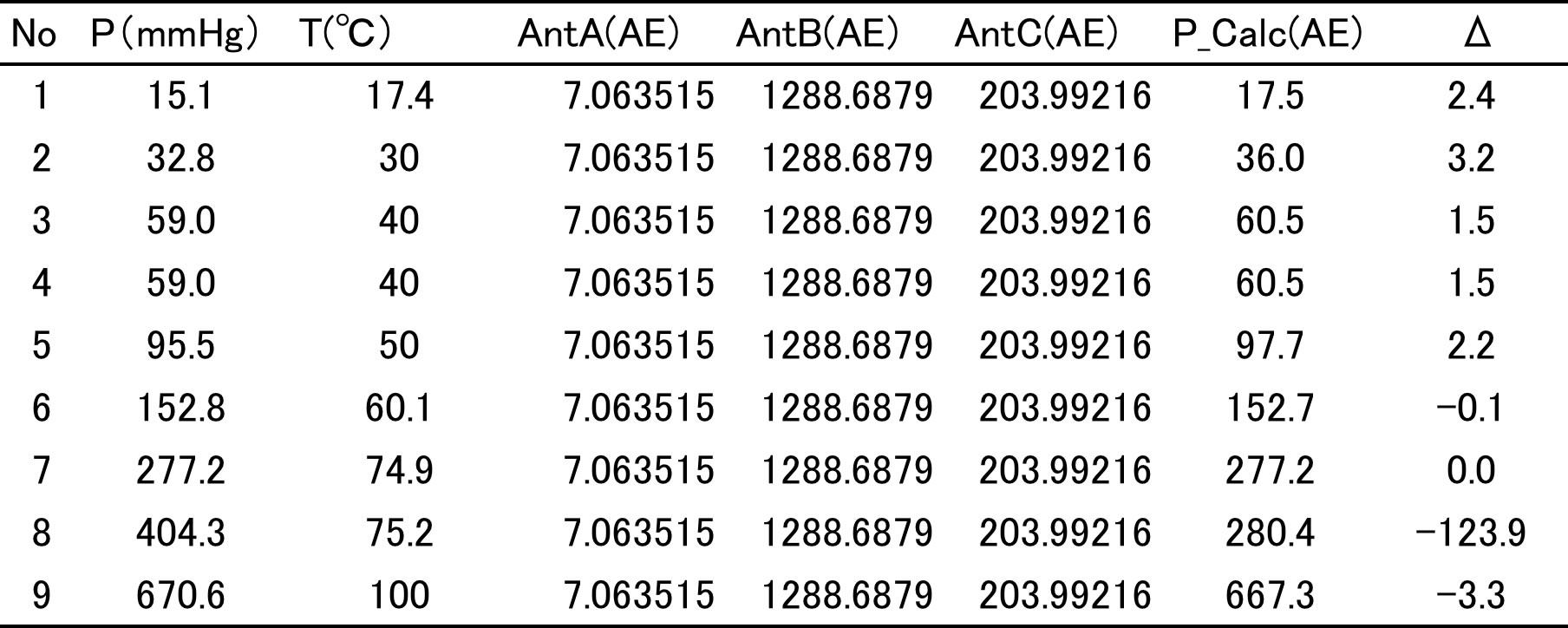
No.8のデータで大きな誤差があります。
実はこのデータはデータベースの誤りか、実験ミスかで正しくないことは下の図をみれば明らかです。チャートを描く手間を惜しんでデータ集を作るとこうなるので気をつけましょう。
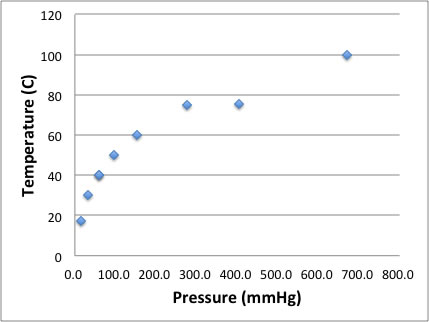
求まったAntoine定数から蒸気圧を計算したのが、P_Calcです。
これも一緒にプロットしてみましょう。
縦横の軸を入れ替えてPressureはlogプロットしてありますが、Antoine定数は非常に綺麗に実験値を再現していることがわかります。
それに対して、最小二乗法を使って計算を行ってみましょう。
(画面はJAVAバージョンです。グラフは出てきません。)
得られたAntoine定数を使って先程と同様、テーブルに埋め込みます。
古いJavaの記述
2012.1.10
JAVAのコピー&ペーストができないという問題が指摘された。これはjava.policyを書き換えればいいそうだ。Windowsを使っているなら、こちらの記事を参照してください。
Macでは、ライブラリー/JAVA/HOMEに行き、そこのsecurityのフォルダーのオーナーに自分を入れて、その中のjava.policyを書き換える。詳しくはこちらの記事を参照(英語)。
grant {
permission java.awt.AWTPermission “accessClipboard”;
};
自分は全部書き換えてしまった。 もとのファイルに付け加えれば良い。(自己責任でやってください!)
2013.2.9 MacでもJava PolicyToolが使えるそうだ。自分のホームディレクトリーに.java.policyを書き込めばシステムのSeculityをいじらなくても変更できる。SafariはローカルのJava Appletを走らせる事ができなくなった。MacのWeb共有を立ち上げて、ライブラリー/WebServer/Documents/にプログラムを置き、http://localhost/から呼び出せば良い。localhostではなくhttp://10.0.1.2/などと入れてしまいお気に入りに登録してしまうと、立ち上げ直した時などに番号が変わる事があり呼び出せなくなる。
| P(mmHg) | T(℃) | AntA(LS) | AntB(LS) | AntC(LS) | P_Calc(LS) | Δ | Δ*Δ |
| 15.1 | 17.4 | 6.7028832 | 1243.946 | 219.557 | 28.4 | 13.3 | 176.7408655 |
| 32.8 | 30 | 6.7028832 | 1243.946 | 219.557 | 52.3 | 19.5 | 379.1380981 |
| 59.0 | 40 | 6.7028832 | 1243.946 | 219.557 | 81.3 | 22.3 | 499.1273913 |
| 59.0 | 40 | 6.7028832 | 1243.946 | 219.557 | 81.3 | 22.3 | 499.1273913 |
| 95.5 | 50 | 6.7028832 | 1243.946 | 219.557 | 122.5 | 27.0 | 728.6271162 |
| 152.8 | 60.1 | 6.7028832 | 1243.946 | 219.557 | 179.8 | 27.0 | 728.4173895 |
| 277.2 | 74.9 | 6.7028832 | 1243.946 | 219.557 | 300.8 | 23.6 | 559.010094 |
| 404.3 | 75.2 | 6.7028832 | 1243.946 | 219.557 | 303.8 | -100.5 | 10092.48218 |
| 670.6 | 100 | 6.7028832 | 1243.946 | 219.557 | 645.9 | -24.7 | 610.2817263 |
| SUM= | 14272.95225 |
この場合は、先程のNo.8のデータの誤差は、-123.9から-100.5に減っています。
ところが、他のデータポイントの誤差はかえって大きくなっていることがわかります。
そして、誤差の2乗和をとると14272.95となります。
先程の誤差の絶対値オプションを使った場合は、-123.9、2乗すると、15351.21になります。
つまり、前提として実験値にエラーはない、誤差は無い場合には、最小二乗法はいいのですが、このようなエラーがある場合にも、-123.9のエラーをなるべく減らそうと動作します。
-123.9から-100.5へと23.4減っただけで2乗和は、14272.95から10092.48と4181も減少します。
そのため、他のデータポイントが10や20誤差が大きくなっても、8ポイント2020で3200、すなわち、4181も減少したのでお釣りが来ることになります。
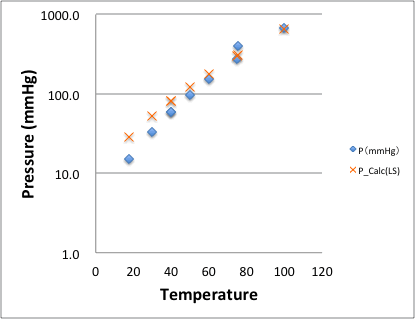
そこで、これをプロットすると上図のように低い温度での誤差の大きいプロットになります。
市販のプロセス・シミュレータはほとんどが最小二乗法を採用しているはずです。
どうしてもそうしたものを使うなら、データはよく吟味して異常値は削除してからフィッティングを行わなければなりません。
さもなければ、こうした、ちゃんと工夫されたソフトウエアーを使わなくてはなりません。
フィッティングがおかしいと感じたら思い出してください。
このAntoine定数の算出の理論的考察はこちらのページを参照してください。
そこでも触れましたが、この方法でAntoine定数を決定すると、分子の構造と定数の間に明確な相関が得られます。
それは何を意味するのかというと、構造からAntoineのBとCのパラメータを予測することができるということです。
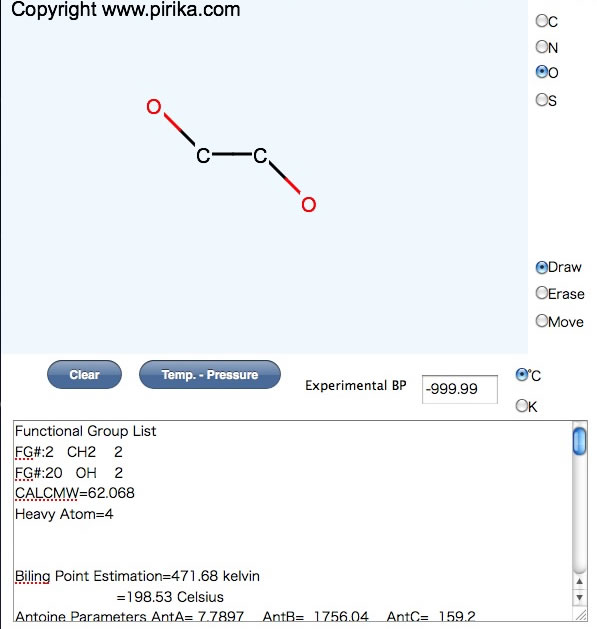
蒸気圧のデータが1点(例えば、沸点-760mmHg)があればAntoineのAも求まり温度全域で蒸気圧が計算できます。
それを行うのがこちらのページです。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
