2022.9.6改訂(2012.7.27)
化学工学トップページ >
ハンセン溶解度パラメータ(HSP: Hansen Solubility Parameters)はC. M. Hansenにより、1967年に発表された。
それ以前にHildebrandによってSP値の基本概念は発表されていた。
しかし、極性溶媒と非極性溶媒が分子の大きさによって同じ1次元軸に乗ってしまうため、これを尺度にして溶解性を議論するには無理があった。
HansenはこのSP値を[δD, δP, δH]に分割した。
δDは分散項と呼ばれ、Van Der Waalsの近接力に基づく項である。
δP項は分極項と呼ばれ、ダイポールモーメント、誘電率などに起因する項である。
dHは水素結合項と呼ばれ、水素結合に基づく分子間力と他には分類できないπ-π相互作用などもここに押し込まれている。
そしてこの [δD, δP, δH] ベクトルが”似たものは似たものを溶かす”というのがHansenの理論である。
HildebrandのSP値とHansenのHSPの間には次の関係がある。
SP値2 =δD2 +δP2 +δH2 式(1)
つまり、図1に示すように、HSPを3次元ベクトルとしてとらえた場合にベクトルの長さがHildebrandのSP値と同じになる。
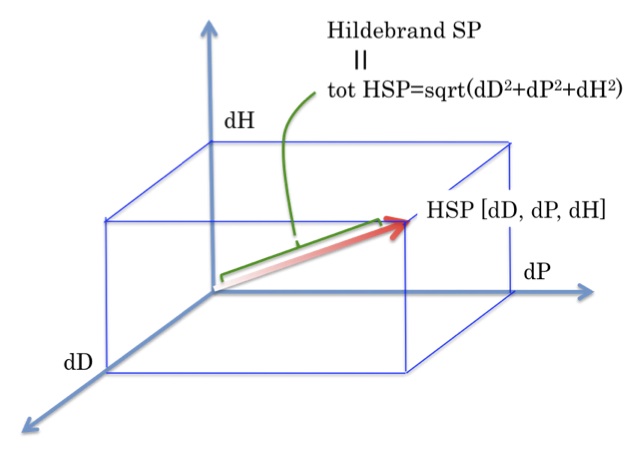
それではこのベクトルの長さは何を示しているのであろうか? これは定義から、
SP値= ((Hv – RT)/Volume)0.5 式(2)
とHv(蒸発潜熱)とVolume(分子体積)から決定される値である。
例えば官能基を持たない炭化水素化合物でも、分子が大きくなるにつれ、Hvは大きくなり、SP値も大きくなるが、HSPではδD項は大きくなるがδP,δH項は0のままになる。
官能基を持つ化合物は一般に分子体積あたりのHvが高くなる。
従ってSP値も大きくなるが、HSPではδP,δH項が大きくなる。
それでは、このベクトルの原点は何を示しているのだろうか? これは蒸発潜熱が0になる点、つまり臨界点を示している。
そこで、ある溶媒のHSPベクトルと溶質のHSPベクトルを比べると言う事は、臨界点を原点にしてベクトルの方向、長さを比較しているということになる。
これはすなわち、対応状態原理(Corresponding State Theory)と同類の考え方であると言って良い。
筆者の一人(山本)は2008年からこのHSPを取り扱うソフトウエアー、HSPiPの開発チームに加わり、新しいアルゴリズムの開発、データベースの維持管理を担当している。
今回はこのデータベースについて解説する。
先にも述べたようにHSPの値を決めるのには、蒸発潜熱、分子体積(=分子量/密度)を知ることは必須である。
蒸発潜熱は蒸気圧の温度微分であるので、正しい蒸気圧式のパラメータも必須である。
HSPの原点は臨界点なので、臨界温度、臨界圧力、臨界体積も重要である。
また、HSPの利用分野の多くが要求する物性値(logKow, 水への溶解度、大気寿命、毒性、生物蓄積性、引火点など)も重要でこれらを含めたデータを管理している。
データの総数は10,000化合物を超えている。
温度依存性のデータはその10倍以上のデータ量になる。
そのうちいわゆる溶媒に相当するものが5割、高分子添加剤、香料など化学品(一部溶媒とも重なる)が3割、残り2割が薬学関連のデータになっている。
薬学関連の化合物は比較的分子が大きく、データとして存在しているのは融点とlogKow、水への溶解度、毒性ぐらいで、あまり化学工学的なデータは存在しない。
残りの8割の化合物については、様々なデータソースをあたり、必要な物性を収集し維持管理を行なっている。
このような化合物データのうち、熱物性で一番多いもので沸点のデータが7000件ほど、logKowで5800件ほどのデータ数しかない。
そこでデータのない化合物については物性推算を行うことになる。例えば熱物性で著名な物性推算法としてはJoback法がある。
これは分子を原子団に分割して、原子団の種類と数から物性を予測する方法である。
我々はこの原子団寄与法に汎用性を持たせるために、分子構造の入力には線形表記法の一種Smiles(Simplified Molecular Input Line Entry Syntax)を採用した。
これらの分子構造のデータはネット上で検索すれば容易に得ることができる。
そしてこのSmilesを解析し原子団の種類と数を決定するアルゴリズムを開発した。
原子団の種類については現在172種類定義されている。
この原子団の定義法であるが、基本的には沸点の推算式を構築し、推算値の合わない化合物の特徴を見た時に、いつも同じ原子団を含む場合に精度が低くなるなどのケースを探し、原子団のタイプを定義し直すという方法を採用している。
例えばアルコール化合物の沸点の推算値がアルキル性とフェノール性で同じOH基でくくっていては精度が低いといった場合、原子団を2種類に拡張するというやり方をとっている。
このやり方を使うと、データベースに登録される構造式はSmiles式なので、分割方法が変わってもデータベース自体は変更する必要がないので便利である。
また様々な分割方法を取り扱いたい場合には、特に便利である。HSPiPで定義されている172種類の原子団はかなり多い方で、Joback法(41原子団)などに変換する場合、変換プログラムを書いてしまえば様々な計算方法の結果を簡単に実装することができる。
化学工学で利用する物性を推算する場合、大まかに分けて2種類の物性があることに注意する必要がある。
一つは沸点のように分子が大きくなるにつれ物性値が大きくなるもので、もう一つは密度のように分子の大きさとは相関が無い物性である。
原子団寄与法は沸点タイプの物性推算には使えるが密度タイプには使えない。
密度タイプの場合には分子の体積(これは沸点タイプ)と分子量から計算するなど工夫が必要になる。
よく見かける間違いは、例えば屈折率の推算に原子団寄与法を使うなどだ。
これは考えてみるとすぐに分かるが、ポリマーのように原子団の数が増えてきた時に原子団寄与法では屈折率がどんどん大きくなってしまうのですぐに間違いがわかる。
それでは溶解度パラメーターはどちらのタイプになるのだろうか? 溶解度パラメータは式(2)で表せるように、体積あたりの蒸発潜熱の1/2乗(ルート)となる。
これは別の言い方をすると凝集エネルギー密度と呼ばれ、密度タイプであるが、それのルートであるのが非常に大きな意味を持つ。
例えば、n-アルカン化合物ではヘキサン(14.9)、オクタン(15.5)、デカン(15.7)と分子が大きくなるにつれ溶解度パラメータは大きくなる。
それは一見すると沸点タイプの物性に思え、原子団寄与法で推算を行っている推算式もある。
しかし、そうした推算式ではポリエチレンを計算しようとした場合、非常に大きな溶解度パラメータになってしまう。分子の小さい領域では沸点タイプ、分子が大きくなるにつれ密度タイプとなる、それを実現できるのがルート関数なのである。
こうした検討は、化学工学の領域では次元解析(物性値の単位が合うように推算式を構築する)として化学工学の分野で多用されてきたが、コンピュータの発展と共に失われつつあるように思う。
また物性推算を行う解析用ソフトウエアーに関しては様々な改良を行った自作のものを利用している。
単純な重回帰法からはじめ、原子団の相互作用を考慮する特殊な重回帰、温度依存性など複雑な非線形性を導入するプログラム、中身がブラックボックス化しがちではあるが、相互作用と非線形性を同時に考慮するニューラルネットワーク法のプログラムを我々自身で開発して物性推算式の構築を行なっている。
このような解析には、MathematicaやExcelなどの統計学のパッケージを利用する事が多いと思われるが、化学には化学特有の問題を含んでいるので単純に純粋数学、純粋統計学を使うと思わぬ失敗につながる。
その例を蒸気圧データのAntoine定数へのフィティング法を例に紹介しよう。
ある化合物のある温度での蒸気圧をプロットすると、化合物独自の曲線を描く。
温度と蒸気圧の関係は非線形であるので複数のパラメータを使ってフィティングが行われる。
最近ではパラメータ数を4,5個使うものが増えつつあるが、まだまだ3パラメータのAntoine蒸気圧式を使うことも多い。
log(P[mmHg])=A-B/(T[℃]+C)
こうした非線形のパラメータ・フィティングでは解は一つとは限らず、事実、Antoine定数はデータ集によって、値も使える温度範囲もまちまちである。
非線形のフィティングを行うプログラム(多くの場合マルカート法を用いる)は熱力学の常識は持ち合わせてはいないので、誤差だけを最小にするように動作する。
それのどこが問題だろうか? 蒸気圧のデータを蒸気圧式にフィティングしたいという時には、測定した温度に限らず任意の温度での蒸気圧を式から計算できるように、蒸気圧式を構築したい、という場合が多いだろう。
それでは、実際問題として温度は全て等価であろうか?
環境問題をやっている研究者にとっては25℃での蒸気圧が重要であろう。
香料関係の研究者は体温付近の蒸気圧が、気液平衡を計算したいなら沸点近辺の蒸気圧が重要である。
このように化学工学で重要な点近傍をより精度高くするといった事が,一般的な統計学ソフトでは行えない。
しかし、このような要請は非常に多い。
また、マルカート法は自乗誤差を最小にしようと動作するため、実験誤差がある系をフィティングしようとすると、パフォーマンスがかえって悪くなるという特徴を持つ。
下図で示すように右から2点目の蒸気圧は明らかに異常値である。これを最小二乗法で解くとXで示したように低温領域で大きな誤差につながる。それは縦軸がlogプロットなので、80℃付近の誤差はmmHgでみると非常に大きい。そこでは平均の値をとり、誤差を減らし、その分を絶対値の小さい領域に持ってくるのでこのような結果になる。
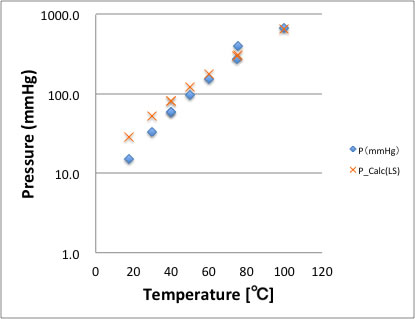
DIPPER801というデータベースは、非常に信頼性が高かく、かつ、信頼性の評価がきちんとしたデータベースであるが、それでも、蒸気圧についてDB中の全化合物について評価した所、(感覚的ではあるが)蒸気圧データ中、5-8%の間ぐらいの頻度で、異常値を見かけた。
化合物が2500個、1化合物あたり、平均30の蒸気圧データがあったとする。
全部で75,000データ。異常値は化合物の7%あったとすると、175個の異常値。75,000データポイントに対しては0.23%のエラーに過ぎない。
しかし、この異常値を含めてAntoine定数を決定してしまうと、2500化合物の7%のAntoine定数は意味が無くなってしまう。
誤差0.23%では済まなくなる。
物理的な実験と比べ、化学の実験値の場合、誤差はつきものである。
そうした誤差に弱い解析手法を盲目的に使う事はさけるべきである。
他には、例えば、ある化合物の水への溶解度を推算する式を作ろうとした場合を考えてみよう。
水への溶解度の実験値は100g/水100gを超えた場合、自由混合としてしてそれ以上実験は行われない。
水への溶解度が100g/水100gというデータベース値があった場合、それが、100g近辺なのか、500なのかは分からない。
従ってそのようなデータを含めて推算式を構築するととんでもない事になる。
引火点のデータでも同じような事がある。>110℃というデータから、不等号が消されて、引火点110℃となっている化合物は多い。
これはデータベースの問題でもある。
つまり、データベースを作成する場合には、その値の属性を決める必要がある。
数値属性のカラムに不等号を入れるとエラーになるので不等号が消えていったという経緯がある。
また、分析手法の進歩の問題もある。
以前では水への溶解度のデータはmg/100gあたりが限界であったが、最近では10^-7 辺りまで正確な値が存在する。
こうした値が混在してしまうと統計処理をして推算式を作ろうとした場合、mgあたりで精度がとても低くなってしまう。
化学工学では実験値に対する有効数字の概念がしっかりしていたが、それを打ち砕いてしまったのが、表計算ソフトであろう。(CASキラーの問題もある。CAS#を日付に変換してしまう問題だ)
こうしたソフトを利用する時代の流れには逆らえないだろうが、利用方法を工夫する余地は残る。
(Dipper801データベースなど信頼のおけるデータベースでは信頼性に関する記述が必ずある。)
これらをきちんと処理できる統計学のソフトを自分は知らないので、自作の”化学”用ソフトウエアを構築し用いている。
こうしたプログラムの作成技術は非常に重要であるが、大学での教育は欧米に比べ非常に遅れているのが現状であろう。
日本でソフトウエアーを自作して解析を行ってるのは、東京大学の船津公人教授のところが著名であろう。
先生の主催されているCACフォーラムに参加するのも問題解決の一つの糸口になるだろう。
それでは、化学者が化学に最適化させた解析ソフトウエアを用いて膨大なデータを処理した場合にどのような”良い事”があるだろうか?
その効果を蒸気圧曲線をフィティングしたAntoine定数を例に説明しよう。
これまでAntoine定数は分子構造からは推算できないとされてきた。
しかし、Antoine蒸気圧式の元になる、Clausius‐Clapeyron式から考えて、AntoineのBパラメータは蒸発潜熱と相関があるべきである。
ln(Pvp)=A-B/T
B=ΔHv/RΔZv
ΔHv:蒸発潜熱,R:気体定数,ΔZv:圧縮係数の差(狭い範囲でBは温度によらず一定)
通常の解析ソフトを用いた場合には、誤差は最小になっているかもしれないが、化学的には意味のないAntoine定数を与えてしまう。
しかし、AntoineのBパラメータが蒸発潜熱と相関があると考えるならば、蒸発潜熱は原子団寄与法で推算が可能であるので、AntoineのBパラメータも分子構造から推算が可能であると考えられる。
その原理を用いて新たなAntoine定数を算出するソフトウエアを作成し、2500化合物以上のAntoine定数を決定し直して見た。
こうして得られたAntoine定数のB,Cパラメータは分子構造と高い相関があり、分子構造から推算することが可能になる。
結果は以下のグラフのようになる。
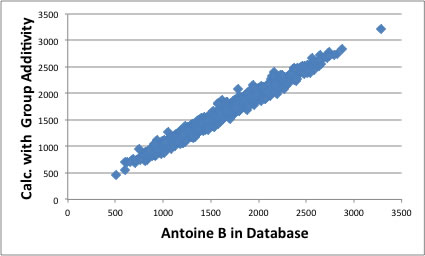
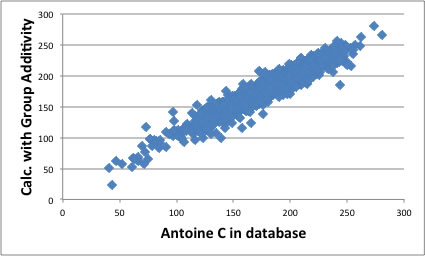
HSPを取り扱うソフトウエアー、HSPiPにはニューラルネットワーク法などを用いて精度高く物性を推算するYMBという機能が搭載されている。
HSPiPが溶解度の分野だけでは無く、化学工学の分野でも広く利用されはじめているのは、”化学”統計学を駆使した解析に基づいているからだろう。
ただし、それをもって学生にとって “良い事”とは言えない。
もし、将来ソフトウエアー開発企業に就職して開発に携わるのなら知っておいたほうが良いとは思うが、化学工学に携わるのなら本当の “良い事”は別のところにある。
それについて説明しよう。
カルボン酸が2つベンゼン環に付加した化合物は、付加した位置によってo-,m-,p-体が存在する。そのAntoine定数を比較してみる。
o- 7.7449 2122.6 111.178
m- 7.7387 2653.5 65.949
p- 7.6750 2876.6 40.552
o-体のAntoineのB定数が他のものと比べ小さい事が分かる。
クラジウス・クラペイロンの式からAntoineのB定数は蒸発潜熱を示すのであれば、フタル酸と比べテレフタル酸は4/3倍蒸発潜熱が高い事が分かる。
このようにベンゼン環1つにカルボン酸2つというほとんど同じような構造をとっていても、対称性の高いp−体は蒸発潜熱が大きくなる。
これは、PETが高い耐熱性や低い印刷性を持つこと、溶融粘度、液晶の相転移温度、可塑剤の融点などを理解する上で欠かせない知識(ナレッジ)で、化学工学を学ぶ者だけがこれらの現象を定量的に理解する事ができる。
このような形で整理されたものの集合体は知識(ナレッジ)・ベースと呼ばれる。
蒸気圧データベースでは2,500化合物*30蒸気圧データ=75,000データが、Antoineの形では、2500*3パラメータ=7500データ、ナレッジ・ベースでは官能基数167*3パラメータで表現でき、しかも、蒸気圧以外の様々な分野で知識としての利用が可能になる。
サイズは1/100以下になり有用度はさらにあがるのがナレッジ・ベースだ。
5定数の蒸気圧式では
o- -90.3221 -3221.4 44.109 -.050056 .000016895
m- 101.893 -12470 -29.146 .0000000121 .0000024529
p- 105.8916 -14001 -30.009 -.000000218 .0000020825
などの値がDBに記載されているが、この値を見ても何もわからないことは明らかだろう。
このAntoine定数を使って太陽電池用の素材を検討した例をこちらに置いたので参照いただきたい。
化学工学が持っている膨大なデータを解析したいという言う時は、個々のデータを知識の形に昇華して扱いたいのであって、個々の精度は高いが、意味の無い数値の羅列で扱いたいのではない。
さもなければ、「働けど、働けど我が暮らし楽にならず、じっと手を見る」という事になりかねない。
逆に言えば現在そうなってしまっているので、化学工学の持つビッグデータの解析が待ち望まれているのかもしれない。
ニューガラスフォーラムの作成しているガラスのデータベース(InterGlad), 物質・材料研究機構が作成している高分子データベース(PolyInfo), 知織化なしには、10万件集めようが、100万件集めようが終わりは無い。
ソフトウエアーを作る事ができれば、ある官能基とある官能基が相互作用して、ある物性値を大きく変える原子団の組を50個見つけろ、などという検討も容易に行う事ができる。
そうした結果は知識として蓄える事ができる。
ある酸化物とある酸化物が組み合わされるとガラスの融点が特異的にさがるとか、レアーアースを使わないと出せない物性が汎用の酸化物の組み合わせで出せるとか。
知織化にはDB化には出せないメリットが非常に多くある。
そうやってコンパクトになったナレッジベースは情報発信を通じて切磋琢磨される必要がある。
例えばJoback法は有機物の物性推算式として非常に著名である。
(Dr. JobackはMITの化学工学の学生の時にこの論文を発表している)
しかし、ハロゲンは原子しか定義されていないので、代替フロンを設計しようとした時には役に立たないのは明らかだろう。
Appenのガラス物性推算式も非常に著名だがレアーアースが入ったら計算ができない。
これらの元の式は公開されているので、自分も含め多くの研究者が、それをベースに改良を加えている。
サイエンスはゼロからの構築である必要は無い(まーノーベル賞はもらえないが)。
先人の行った研究に、より般化した式、より広く適用できる式、より精度の高い式を構築していく。
それが人類の進歩だ。常にゼロから行かなければならないのであれば、人類の進歩は止まってしまうだろう。
特にコンピュータ系の仕事の場合、論文は公開しても、プログラムは公開されない事が多い。
複雑な数式を駆使してインパクトファクターの高い論文に掲載されても、査読さえ通ってしまえば、その後、切磋琢磨されるかどうかはわからない。
いろいろな立場の研究者がモデルを叩き合って切磋琢磨していく、それには論文よりもWebの方が適していると思う。
Pirikaでは1999年からJAVAを使ったインターラクティブな情報公開を始め、去年2011年にはHTML5を使ったものへと着実に進化を遂げている。
そして、世界の一線級の研究者と自分の作った式について議論し、改良し、再び発信するを繰り返している。
常に目を光らせ、新しい技術を取り入れていかない限り、情報発信者としての評価を得続ける事はできない。
そういう努力はせずに、あーだから駄目、こーだから駄目と評論してくださる方はたくさんいる。
でも、Googleは正直だ。力を入れている分野はランクが高く、ほうり返している分野はランクが低くなる。
選択と集中、個人のサイトであっても正しい事だと思う。
またどんなに下手でも良いから英語のページを作るのは必須だろう。文字通り桁が変わる。
以上のように、
- 情報収集(データベースの構築技術 )
- 情報解析(物性推算式の構築技術 )
- 情報集約(知識ベース[ナレッジ・ベース]化技術 )
- 情報発信技術
化学工学を学ぶ研究者がこれらの技術を身につけた時に、”製造業における研究開発に化学工学者は欠かせない”と言われるような時代が来ると確信している。
化学を取り扱う解析用ソフトウエアーは化学者が作るべき。その例をグリーンソルベントの製造プロセスで紹介した。参照いただきたい。
他の例は、大学での講義ノートを置いてあるので参照して頂きたい。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
