2013.4.17
化学工学トップページ >
マランゴニ数 (環境工学研究所資料): マランゴニ数は2つの流体が接した界面で起こる表面張力の局所的な不均一によって生じるマランゴニ対流を支配する無次元数。
これはインクジェットを使って液滴を作った時に、いかに均質な膜厚のコーティングを作るか?を理解する上で非常に重要な物性値だそうだ。
自分も初めて聞いた無次元数であるが、海外の研究者からの問い合わせが相次ぎ、あわてて勉強した。
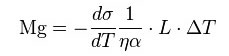
σ: surface tension, (SI units: N/m)
L: characteristic length, (SI units: m)
α: thermal diffusivity, (SI units: m²/s)
η: dynamic viscosity, (SI units: kg/(s·m))
ΔT: temperature difference, (SI units: K)
熱拡散率という聞きなれない物性値が必要だったので難しいかと思ったが、次式で計算できることが解った。
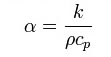
k is thermal conductivity (W/(m·K))
ρ is density (kg/m³)
Cp is specific heat capacity (J/(kg·K))
つまり、表面張力、粘度、密度、熱伝導率、熱容量の5つの物性値の温度依存性が計算出来ればMgは計算で出すことが出来る。
こうした物性値の推算法はpirikaでも扱っているので参照して欲しい。
プログラムは、HTML5という技術を用いて作成されている。
2013.4.18 Dynamic ViscosityとKinetic Viscosityを間違って取り扱っていました。
粘度と動粘度、取り違いが多いですね。Dynamic Viscosityというと訳す時に動粘度って訳してしまいがちですが、正しくはKinetic Viscosity=動粘度です。
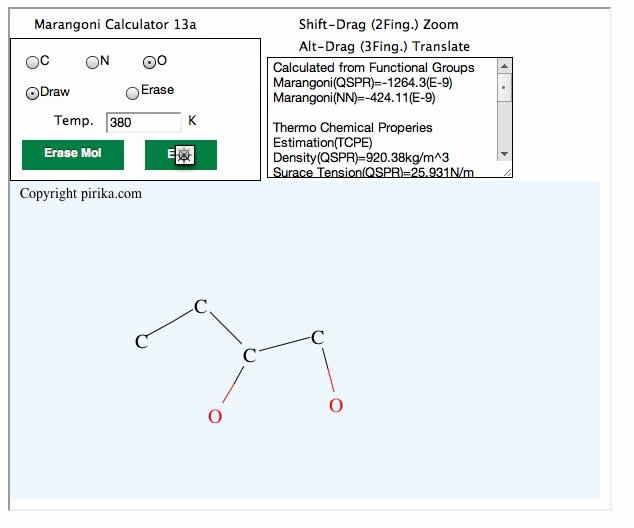
正しいブラウザーを使ってこのページアクセスすると、上記画面が現れるので分子を描き、温度をセットしてEXEボタンを押す。
詳しい分子の描き方はこちらを参照してください。
計算結果を全選択して、メモ帳などにペーストする。
このプログラムではマランゴニ数を3つの方法で推算する。
QSPR法とニューラルネットワーク法は、描かれた分子を原子団に分割し、温度と原子団の情報から直接マランゴニ数を推算してしまう。
何故そのようなことをするのかは講義の時に話そう。
ヒントはある溶媒があった時、そのマランゴニ数がいくつになるか、分子構造を見ただけで人間が見当がつくか?
温度を変えた時にどちらにずれるか見当がつくか?
という事だ。
この方法はパラメータが決定されていない原子団を使うと計算が失敗する。
原子団は全部で167種類定義されているが、マランゴニ数の元データ(文献値とその依存性)は300種類程度の化合物から作ったので、使われていない原子団も多数ある。
もう一つの方法は5つの物性値とその温度依存性を推算して元の式からマランゴニ数を計算するものだ。
Pirikaの物性推算式は167原子団全部についてパラメータが揃っているので、その原子団の範囲であれば物性値は全て計算することができる。
しかし各々の推算式には当然誤差が含まれる。それが悪い方向へ重なった場合には大きな誤差になってしまう。
現時点ではどちらがいいかは解らない。
計算結果は次の形で出力される。
Calculated from Functional Groups
Marangoni(QSPR)=2727.8E3L(m)ΔT(K)
Marangoni(NN)=1202.56E3L(m)ΔT(K)
Thermo Chemical Properies Estimation(TCPE)
Density=998.42 kg/m^3
Surace Tension=0.03502868722926647 N/m
dST/dT=0.00011465796347992843 N/m・K
Viscosity=0.008778151688884428 Pa・S
Heat Capacity=2499.906019755444 J/(Kg・K)
Thermal Conductivity=0.19045005622351197 W/(m・K)
Thermal diffusivity=7.630378671337975e-8 m^2/s
Marangoni=-171.18 E3L(m)*ΔT(K)
QSPRを使って、元データを解析した結果は次のようになる。
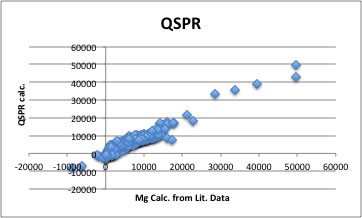
ニューラルネットワーク(NN)を使ったものの方がよく収束している。
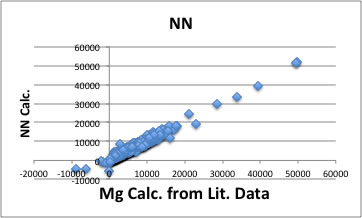
実際にどう使うのかは、自分の分野とは余りにかけ離れているので正しいことは言えない。
例えばインクジェットで、基板の温度を変えて塗布実験をする。
どの温度の時に一番均質な膜ができたか見て、その時のマランゴニ数を控える。
溶媒を変えた時には、その控えたマランゴニ数の周辺になるように温度を調整し実験をする。
そんなところだろうか?
YouTubeの映像、インクジェット着滴後の乾燥&コーヒーステイン現象を見て頂きたい。
コーヒー・ステインというのは、コーヒーの液滴が乾く時に、中央部よりも周辺部にコーヒーの濃い模様が現れる現象のことだ。
これはマランゴニ対流で説明される。
こんな乾き方をしたらナノ配線の導電性は解釈が難しくなるだろう。
用途によってインクジェットで飛ばしたいものは変わるだろう。
単純には顔料だろうが、量子ドット用のCdSだったり、ナノ配線用のAg,Cuだったり、有機EL用の化合物だったり。
それらの溶解(分散)溶媒は多岐にわたっており、当然毒性の高いものは他の溶媒に置き換え無くてはならないし、コストやハンドリングのしやすさも重要であろう。
インクジェットも圧力式なら温度は変わらないが、バブルジェットでは液滴の温度も変わる。
そうした時にいわゆるグリーンソルベントから必要なマランゴニ数になる溶媒の種類と温度が見当がつけば研究の加速が図られるというのが、海外の研究者がこのパラメータの推算式を欲しがっている理由の一つだろう。
海外の研究者から問い合わせが多く、新しいHSPiPがでるまで待てないと言われて、暫定的に原子団をフルセットに拡張した新バージョンを限定公開した。
HSPiPのユーザーの方には、メールを頂ければそのURLをお知らせします。(フィードバック次第ではあるがHSPiPには当分搭載されないかもしれない。)
超臨界炭酸ガスへの有機物の溶解性を調べていた所、マランゴニ数が重要な役割を果たしていることがわかってきた。
超臨界や乳化などは一種の無重力状態でこうした対流が影響をあたえるのかもしれない。
自分はこの物性値に関しては全くの素人なのだが、HSPiPチームのAbbott教授がHPで解説を行なっている。
英語に不慣れな人用に簡単に翻訳しておこう。(計算機もあるので是非訪れてみてください)
マランゴニ数(Ma:Marangoni Number)は、コーティングに対して自発的に生成する表面張力によって駆動される対流の傾向を捉える指標だ。
極端なケースでは完璧な6角形(ベナードセル)の紋様をコーティングに生成し、一般的に言って(特にインクジェットでの)印刷/プリント層を台無しにしてしまう。
Ma=δσ/δTLΔT/(μ.α)
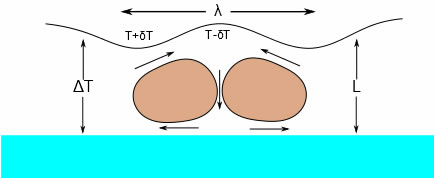
これが何を意味するかというと、表面張力の温度変化率(δσ/δT)が大きくなれば、表面張力の変化によって駆動される対流も大きくなる。
もちろん、コーティング/プリント層から表面までの温度変化(ΔT)が大きくなっても、対流は大きくなる。
コーティング層が厚い (L)と結果はより悪くなる。
ベナール・セル(茶色の部分)が対流によって生成されていることが示される。
流れの矢印の方向に従って、表面張力は T=T+δTの時より小さく、T=T+δTの時より大きくなる。
セルの波長 λ はλ=2πL/√(Ma/8)で与えられる。
高粘度 (μ) と高い熱拡散 (α)を持つ液体を使うことによってマランゴニ数を減らすことが出来る。
粘度の効果は明らかだろう。
高い熱拡散は、温度勾配の効果が急激に減少する事を意味している。
典型的な値は δσ/δTで 0.1 mN/m/°C、温度差 10°C、粘度 5cP あたりだ。
我々の多くはこれらの正確な値を得ることが出来るだろう、問題はαの値だ。
単位として便利なmm²/sを使った場合、Water=0.14, Ethanol=0.07, Acetone=0.083、多くのアルカン、アルケン、芳香族で0.08-0.09のあたりになる。
マランゴニ数としてはどんな値が欲しいのだろうか?
”できるかぎり小さな値”だろう。
コーティングがどれだけ早く乾燥/固化するかに依存し、それが早ければマランゴニ対流が問題を引き起こす時間的余地を与えないだろう。
しかしプロセスが遅ければ、完璧なコーティングを得るのには小さなマランゴニ数が必要だ。
公式の答えとしてはマランゴニ数<80で不安定さはなくなるが、現実問題としては40付近でも不安定なこともある。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
