2024.9.9
pirika.comで化学 > 化学全般 > 高分子化学 >
MO計算による活性化エネルギーと頻度因子の推算
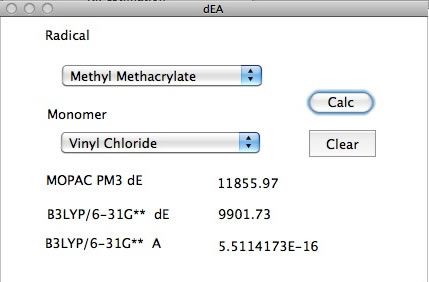
ラジカルとモノマーを選んで計算ボタンを押すだけだ。
実際にやってみよう。左側がラジカルで右側がモノマーだ。
以降、2004.9.17の古い記述。
この計算には、MOPAC、PM3レベルで、ラジカルのSOMO, HOMO, そしてモノマーのHOMO、LUMOと2重結合の電荷だけを使う。新しいモノマー、ラジカルの組み合わせを導入するのが非常に簡単で、しかもB3LYP6-31G**レベルの計算結果が得られるので有用だった。
画像は古いJAVAのプログラムのものだ(2011.11.23、MacのSafariブラウザーでは動作した)中身はそのままJavaScriptに書き直したものだ。
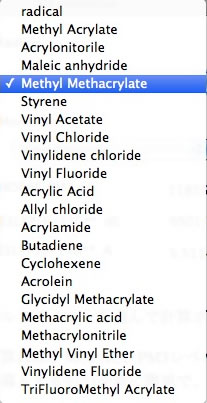
現在(当時)このようなモノマーが登録されている。
ポイントは、新しいモノマーを追加するときに必要な物性は、MOPACでラジカルとモノマーを各々計算するするだけでいいということだ。他のモノマーと組み合わさった時の活性化エネルギーと頻度因子はニューラルネットワークが推算する。
現在のpirikaではQe値を用いたシユレーションを使っている。それに対するこの方法のメリットは反応の温度をあらわに使って計算するところだろうか。
Qe値の場合は、r1=K11/K12と反応速度定数の比になってしまうので、温度は変わっても相殺されてしまうと考える。
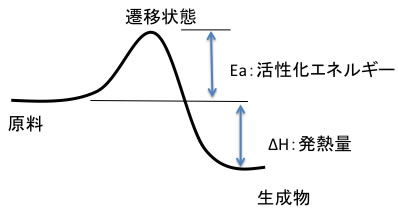
通常の化学反応では、下図のような反応プロファイルをとる。
一般的には発熱量の大きいものは反応は進みやすい。
しかし、活性化エネルギーが非常に高ければ反応は進みにくい。この活性化エネルギーを求めるには、実験的には温度を変えた実験を数点行い、アレニウス・プロットをし、その傾きと切片から活性化エネルギーと頻度因子を計算する。
Kを反応速度定数、Aを頻度因子、Rをガス定数とすると、アーレニウス式は次のようになる。
k=A・e(- Ea / RT)
分子軌道法でも、ガウシアンを使い、基底関数をそれなりに高いものを使い遷移状態を求めれば、かなり精度よく活性化エネルギーを計算する事ができる。(藤本博、有機反応と軌道概念、化学同人、1986)
2分子反応の速度式は次のように書くことができる。(1分子の場合どういう式になるか確認しよう)

そこで、遷移状態を求め、エントロピー項(dS)とエンタルピー項(Ea)を求め、Kを計算してしまうことができる。MOPACの場合、分子の振動解析の結果があまり正しくないので、頻度因子は正しく求まらない。
pirika.comで化学 > 化学全般 > 高分子化学 >
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
