2024.9.27
物性化学トップページ
Pirikaで提供するプログラム
2011-2024年横浜国大(YNU)で行なった授業で使ったYNU-YMBを公開した。
重原子は15まで、CHNO以外の原子は1以下。パラメータは2013年のものなので古い。JSMEの使い方はこちらを参照して欲しい。
以降、2011.6.24の古い記述。
YMBシミュレータ(HTML5 プログラム 2011.6.10)
web版でPass Codeを持たない場合、重原子4つまでしか計算できない。Pass Codeがあるなら、精度も高く、蒸発潜熱の温度依存性も計算することができる。
シス、トランス化合物はその平均値を返します。
芳香族用のパラメター、ハロゲン化合物のパラメーターは入っていません。
(分子の描き方はこちらを参照してください。)
Joback法ーHTML5バージョン(統合化バージョン 2011.4.16)
最新の推算方法は、HSPiPに搭載されている。HSPiPに搭載の商用版では、F, Cl, Br, I,S, P, B, Siが使える。芳香族も扱え、最大重原子数は120になる。
プログラムによってどんな原子団が使えるかはこちらで確認のこと
推算法
蒸発潜熱の推算法で著名なのは、Joback法(Wiki Pedia)であろう。
これは原子団寄与法で沸点における蒸発潜熱を推算する。
実はこの方法は最近知ったもので、どのくらいの精度で推算できるかは検証したことがない。
しかし、沸点における蒸発潜熱が原子団寄与法で推算できるということは、原子団の効果が沸点に於いては同一で、分子によらないということになり非常に興味深い。
佐藤一雄先生の物性推算法の中でも、物性を臨界点からの距離で見るような対応状態原理よりも、物性によっては沸点をベースに考えたほうが有効であると指摘されている。色々な見方をするべきだろう。
沸騰の科学についてまとめた。こちらから参照してほしい。蒸発潜熱に関する記載も多いので参考になると思う。
Joback法とは違うが、原子団寄与法で蒸発潜熱を推算する式を構築して、精度を検証したことがある。
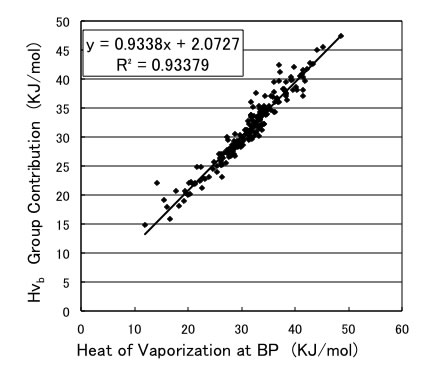
沸点における蒸発潜熱はこのぐらいの精度で推算できたので、Joback法でも同じくらいだと思われる。
対応状態原理を用いて蒸発潜熱を推算する式もいくつか開発されている。
対応状態原理を用いて蒸発潜熱を計算するには、沸点や臨界定数が必要になる。
推算値を使う場合にはこちらを参照してほしい。
著名なものはVetre法だろう。これは次式で沸点における蒸発潜熱を推算する。
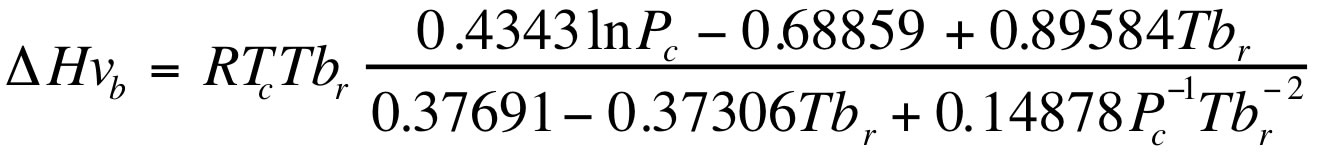
この式を使って”The Properties of Gases & Liquids”にあるデータを検証すると以下のようになる。
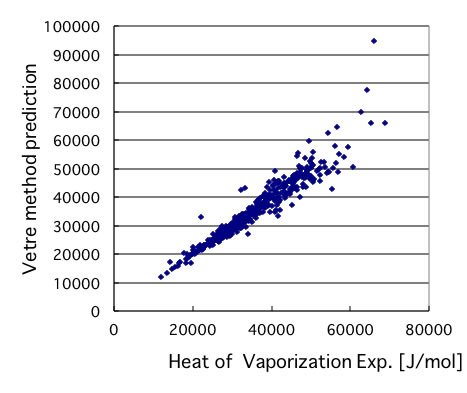
蒸発潜熱の高い領域で精度が低い。
ニューラルネットワーク法で推算式を構築したものがPirikaのHPに掲載されているが、その場合の精度は次のようになる。
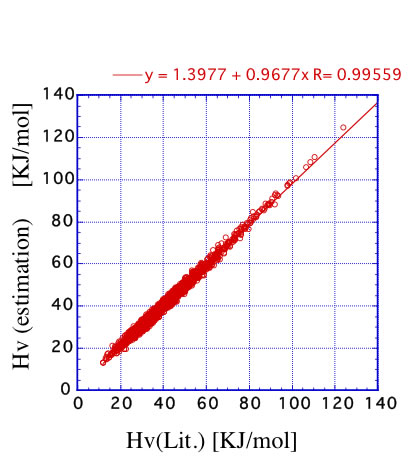
この蒸発潜熱も温度の関数で、温度が上昇するに連れ値は小さくなり、臨界点では0になる。アセトンの実験値の場合には次のようになる。
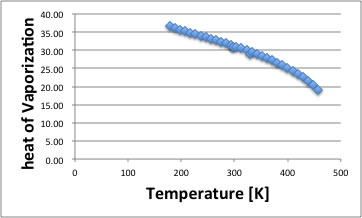
沸点における蒸発潜熱を25℃に変換するには,Watson式を使う。
dHv2=dHv1((1-Tr2)/(1-Tr1))0.375
dHv1:沸点における蒸発潜熱,Tr1:沸点/臨界温度,Tr2:任意の温度/臨界温度,dHv2: 任意の温度における蒸発潜熱
この式を使い、Vetreの所で示したデータを25℃に変換し、25度の実験値に対してプロットすると以下のようになる。
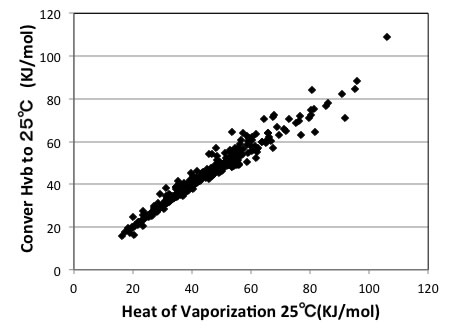
さらに他の対応状態原理法である、Pitzer-Carruth-Kobayashi 法は直接、任意の温度での蒸発潜熱を推算することができる。これは以下の式を使う。

その精度を検証してみると次のような結果となる。
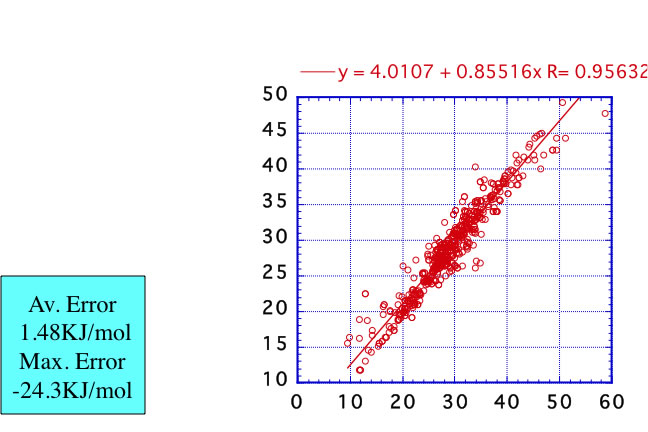
この温度依存性をさらに詳しく見てみよう。
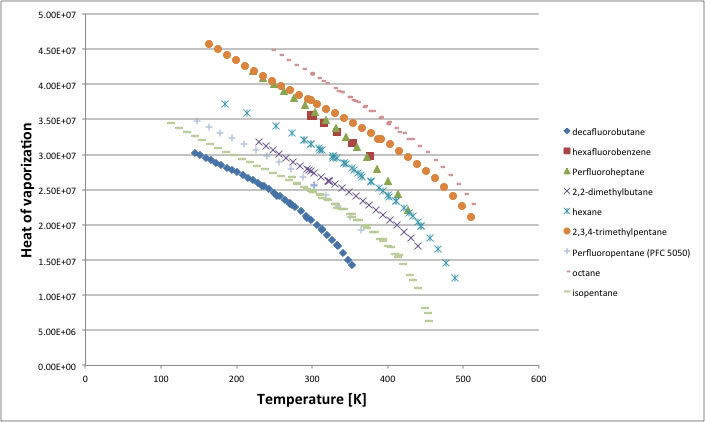
いくつかの非極性化合物について蒸発潜熱の温度依存性を取り出してグラフに書くと上図のようになる。
蒸発潜熱は臨界温度で0になるので、このグラフを臨界温度からの相対距離(1-Tr)で整理してみる。
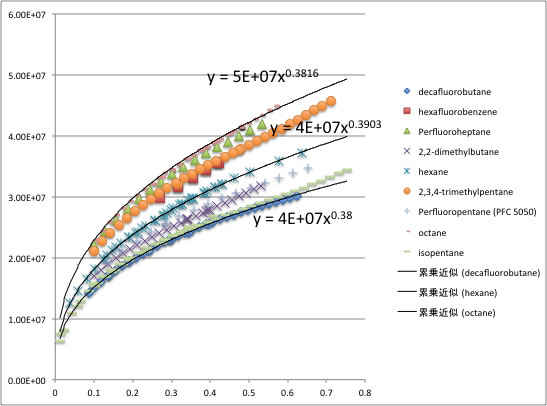
すると、(1-Tr)の指数項は0.38-0.39の範囲に入ることが判る。
これがWatson式で0.375を採用していることの根拠になる。
ある温度での実験値が一つでもあれば、指数の前の係数はキャンセルされるので温度依存性を推算できる。
Pitzer-Carruth-Kobayashi 法でも(1-Tr)の指数項は0.354と似たような値になる。
臨界定数は入手が困難な事を考えると、沸点における蒸発潜熱を精度高く推算してWatson式に持って行くほうが有利である。
そこでさらに沸点における蒸発潜熱を詳しく見てみよう。
”The Properties of Gases & Liquids”にある沸点における蒸発潜熱のデータを沸点に対してプロットすると下のようなグラフになる。多くの化合物で直線に乗る。この関係はTroutonの通則として知られている。
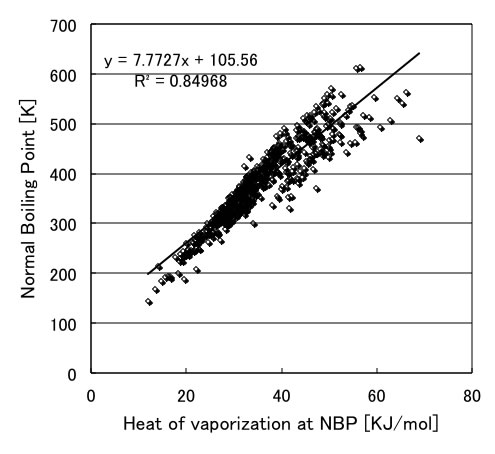
Troutonの通則によれば、無極性液体の沸点における蒸発潜熱(Lb)はその標準沸点(Tb)と相関があるとされている。
Lb/Tb=21 cal/g-mol
それを修正した,Kistiakowskiの式では,
Lb/Tb=8.75+4.571*logTb
とした時に誤差は±3%以内であるとされている。しかしこれらの式は極性分子には適用できない。極性分子に関しては,Watson-根岸の方法にあるように,化合物ごとに補正係数を入れる事によって蒸発潜熱を推算する。実際にいくつかの化合物についてみてみよう。
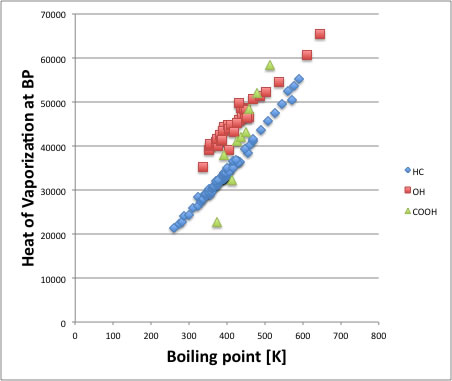
HC(炭化水素化合物)については沸点と蒸発潜熱には非常にきれいな関係があることがわかる。
アルコール化合物に関してはHC化合物の直線とほぼ平行でるので、アルコールの補正係数を決定すれば一つの式で扱えるだろう。困りものなのはカルボキシル基を持った化合物だ。
それ以外の化合物、オレフィン、エーテル、ケトン、エステルなどは、ほとんどHC(炭化水素化合物)の直線に一致する。
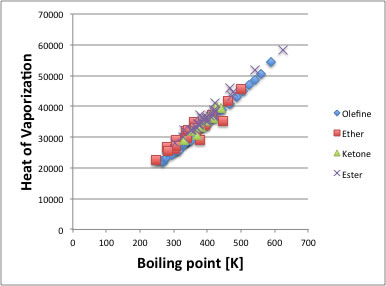
ここで、Troutonの通則から外れるのは、水素結合のエネルギーによるのだろうと分かる。(この原理を用いると分子の水素結合エネルギーの評価を行うことができる。)
そこでカルボキシル基の異常性が理解できる。低分子量のカルボン酸はダイマーとして蒸発する。
そこで、官能基を持たない同じ沸点の炭化水素化合物よりも低い蒸発潜熱しかもたない。
分子量が上がるに連れて、ダイマーで蒸発する割合は減り、最後はアルコールと同等の水素結合性化合物と同じような線上に乗ってくる。
最終的にYMBシミュレータに搭載したのは、原子団寄与法をベースにした非線形式で以下の性能を持つ。
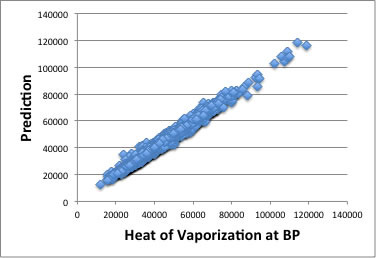
現在のところ、温度依存性を見積もる新しい推算式はつくっていないが、差し当たってはWatson式で十分であろう。
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
