2013.8.15
物性化学トップページ
Pirikaで提供するプログラム
2011-2024年横浜国大(YNU)で行なった授業で使ったYNU-YMBを公開した。
重原子は15まで、CHNO以外の原子は1以下。パラメータは2013年のものなので古い。JSMEの使い方はこちらを参照して欲しい。
最新の推算方法は、HSPiPに搭載されている。HSPiPに搭載の商用版では、F, Cl, Br, I,S, P, B, Siが使える。芳香族も扱え、最大重原子数は120になる。
プログラムによってどんな原子団が使えるかはこちらで確認のこと
屈折率の推算その2
屈折率(n)やモル屈折(RD)は分子が光とどのように相互作用するかを示す。
屈折率は真空中の光の速さ (c)と媒体中の光の速さ (v)の比で表される。
n = c/v
これは無次元のパラメータで有機化合物の多くは、1.3から1.5の間になる。
屈折率は単色光、典型的にはsodium D line(波長 l = 589.3 nm)の黄色光を使って測定される。そして、n20Dのように記載され、これはナトリウムの D線を使って、20°Cで測定されたことを示す。
他の波長としては水素のC線(l = 656.3 nm)もしくはF線(486.1 nm)、水銀のG線( l = 435.8 nm)が使われる。
モル屈折(RD)は、媒体の密度rの関数である。ローレンツーローレンツ( Lorentz-Lorenz)の式はRD、r,nのあいだの関係を電磁気学的な理論に基づいて表す。
RD =(n2 -1)/(n2 +2) * M/ r
ここで、Mは分子量を表し、RDは体積の単位になる。(固有屈折率はRDをMで割ったものになる)
分子屈折RDは屈折率測定波長が同じであれば、気体・液体・固体などの物質状態に依存しないので、屈折率nか密度rの一方とRDがわかればもう一方は推算する事ができる。
例えばRDと密度がわかれば屈折率は次式で計算する事ができる。
n = sqrt((M+2 r RD)/(M- r RD))
この分子屈折RDは分子を構成する原子団に加算値を割り振り、原子団寄与法で推算する事ができる。(屈折率自体を原子団寄与法で推算している例もあるが、高分子を考えれば当然判るが原子団の数が多くなると屈折率はどんどん高くなるので間違いである。RDの単位が体積なので原子団寄与法で推算できる)
分子をさらに細かく分けて原子の数からだけでRDを推算してしまおうという考え方が原子屈折の考え方だ。
各原子に寄与率を割り振って分子中の原子の数だけからRDを推算する。
例えば化学便覧の第14章には原子屈折と原子分散の一覧表が記載されている。
| 原子 | 原子屈折 | ファンデルワールス半径 |
| 水素 | 1.028 | 120 |
| フッ素 | 0.81 | 135 |
| 塩素 | 5.844 | 181 |
| 臭素 | 8.741 | 195 |
| ヨウ素 | 13.954 | 215 |
この原子屈折と原子のファンデルワールス半径[pm]をプロットすると
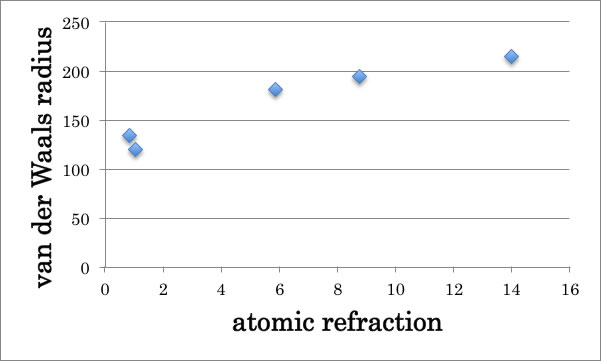
きれいな相関があるため、屈折率(本質は媒体中の光の速さ)は、媒体のファンデルワールス相互作用に相関しているという考え方も成立しているようだ。
水素とフッ素は原子屈折の値は近いが、フッ素化合物は密度が非常に高いためフッ素化合物の屈折率自体は小さな値になる。
水素やハロゲン原子は1価なので簡単だが、酸素、硫黄や窒素などは複雑な結合を作る。例えば酸素原子などはアルコール、エーテル、カルボニルによって原子屈折の値を変えなくてはならない。
| 原子 | 状態 | 原子屈折 |
| O | -O-(H) | 1.518 |
| -O- | 1.764 | |
| =O | 2.211 |
化学便覧には窒素の5種類ぐらいしか無いが、Langeのハンドブックを見ると20種類以上の窒素の原子屈折の値が記載されている。
こうした取り扱い自体は原子屈折を原子団屈折に拡張しただけと見なせるので、余り問題は無いように思える。
どう考えていいのか困ってしまうのが、2重結合や3重結合にまで原子屈折の値が割り振られている事だ。
例えば炭素が6個の化合物でベンゼン、シクロヘキサン、ヘキサンを比べてみると、ベンゼン環は大きな屈折率を持っている事がわかる。
| Name | n | MW | Density | RD |
| benzene | 1.501 | 78.114 | 0.879 | 26.18 |
| cyclohexane | 1.4235 | 84.161 | 0.779 | 27.54 |
| hexane | 1.3723 | 86.177 | 0.659 | 29.74 |
しかし、密度まで加味したRDで見ると、値は大きく変わらず、わずかであるがヘキサンの方が大きな値になる。
それにしても、水素の数は6, 10, 12と増えるので水素の数が増えた事による加算値、1.028水素の数に相当する、2重結合の数(3)2重結合の補正値=1.575を入れないと結果が合わなくなったのだろう。
ある原子が媒体中に存在すると、ファンデルワールス半径という原子の大きさによって光の速度が変化する。
密度が高くなると媒体中で原子と相互作用する光も増えるので屈折率は高くなる。
では2重結合は媒体中で何をしているのだろう?
Langeのハンドブックでは3員環や4員環の原子屈折の加算値が記載されている。
シクロヘキサンとヘキサンのRDの差は、水素(1.028)が2つ分と考えれば説明がつくので、6員環には補正値はいらないのだろうが、何故ひずみの大きな環は密度以上の補正が必要になるのだろうか?
こうした結合次数や環の大きさの補正は原子屈折とは相容れない気がしてしょうがない。
そこで、Organic Solvents(4th Edition)にある溶媒と298.15Kにおける屈折率のデータに対して解析を試みた。
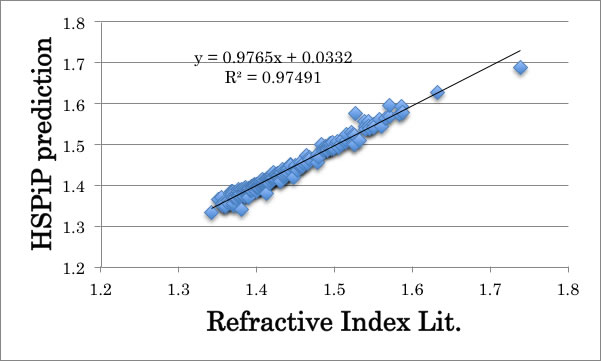
HSPiPには、分子を原子団(167種類)に分割し屈折率を推算する機能が搭載されている。
これは原子団ごとの加算値を文献値から定め、密度の推算値と合わせて屈折率を試算する。
上の図で大きく外れるものは、ヨウ化メチル(CH3I)である。この化合物が大きくずれるのは、CH3Iを原子団に分割する際に、CH3+Iに分割するのだが、CH3は非常に多くの化合物に使われる原子団で、その平均値を加算値として使っているためであると考えられる。
次にHSPiPで算出した分子体積(実験値ではなく推算値)を使って、屈折率から分子屈折RDを求める。
そのRDの値を再現するように、まず最初に原子の数のみから推算式を構築してみる。
Organic Solventsに記載のあるデータのうち有効なものは229化合物分あった。
| Hcode | (n^2-1)/(n^2+2)*Mvol | C# | H# | Br# | Cl# | F# | I# | N# | O# | S# |
| 303 | 24.18310878 | 2 | 6 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1021 | 41.32190037 | 7 | 7 | 0 | 0 | 0 | 0 | 1 | 3 | 0 |
| 900 | 42.75388212 | 10 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 604 | 36.82166188 | 8 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 851 | 35.16177053 | 8 | 7 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 867 | 53.32450722 | 12 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
そして。屈折率nの値とMVol、分子中の原子の数から上のようなテーブルを作り、2列目を目的変数にして重回帰計算を行い、各原子の重回帰係数を求める。
(n^2 -1)/(n^2 +2)*Mvol= 3.7710*C#+0.4106*H#+8.2263*Br#+5.4481*Cl#+0.2692*F#+13.5379*I#+3.1246*N#+1.7385*O#+8.3597*S#+1.06047
となった。
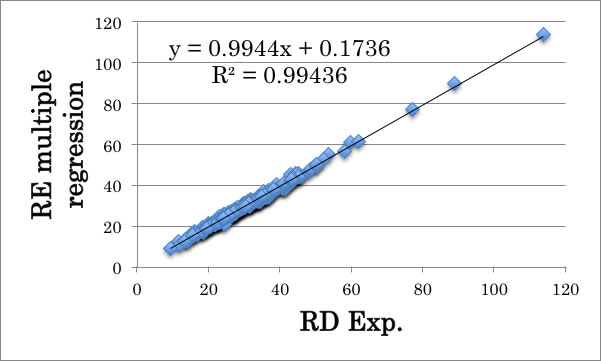
相関係数の自乗は0.99436であるので非常に良好にRDを計算できている事が判る。
ここで求まった各原子の重回帰係数をファンデルワールス半径に対してプロットすると、先ほどのハロゲンの時と同様にきれいな相関が得られるので重回帰係数と原子屈折の加算値は同じ意味合いを持っていると考えてよい。
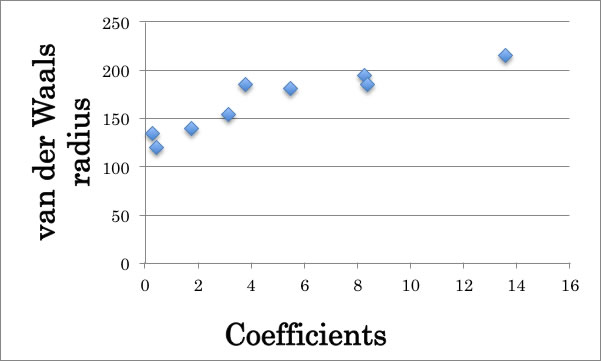
それでは、ここで求まった推算値のRDとMVolの値から屈折率を求め、文献値の屈折率と比較してみよう。
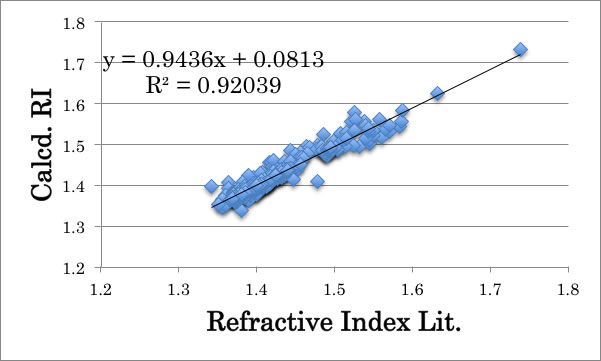
RDのR2 は0.99436と非常に高かったにも関わらず、それを屈折率に戻すとR2 は0.92039と精度は大きく低下してしまう。
それはRDを計算する時に(n2 -1)/(n2 +2)と屈折率を自乗しているので、RDの誤差が圧縮されてしまうためだ。
そこでRDの推算式はさらに高い推算精度が要求される。
精度を上げるために、結合次数や環の大きさの補正を入れるのであれば、化学便覧やLangeのハンドブックと同じ事で、“原子屈折”という考え方に矛盾してしまうので、他の項を導入する事を考える。
まず最初にやることは、どんな化合物が合わないのかを特定する。 (この作業は物性推算式を構築する際は、繰り返し行う)
| RI(lit.) – RI(Calc) | Name |
| 0.06795 | dimethyl sulfoxide DMSO |
| 0.04282 | o-nitroanisole |
| -0.03294 | alpha-pinene |
| 0.03624 | 1,2-Dimethoxybenzene |
| 0.04044 | styrene |
| -0.03696 | Phenyl Acetonitrile |
| -0.02132 | bicyclohexyl |
| -0.05360 | thiophene |
| -0.02495 | trans-decahydronaphthalene |
| 0.03766 | o-toluidine |
| -0.04129 | methyl cyanoacetate |
| 0.03448 | o-cresol |
| 0.02007 | 2,2,3-trimethylpentane |
| -0.01933 | dibenzyl ether |
| 0.03912 | aniline |
| -0.04449 | chloroform |
| -0.04351 | propionitrile |
| -0.05631 | acetonitrile |
| -0.02528 | hexanenitrile |
| -0.01929 | octanenitrile |
まず、DMSOが合わない(上のグラフで真ん中付近の外れているもの)。
篠田耕三、「合成と溶解のための溶媒」丸善(1969)にその理由が記載されている。古い本で絶版なので引用させていただくと、DMSOの特徴は

で表されるS→Oの半極性結合にある。
この結合のためDMSOは低温では下のように会合した形で存在すると言われるが、温度が上昇すると解離し、比重、屈折率などの物性定数も変化する。
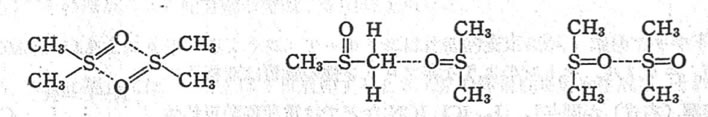
とある。そこで取りあえずDMSOはこの検討から除外する事にする。
次に特徴的なのは、ニトリル基を持つ化合物が6つ、いずれも計算値が大きくなってしまう。
これが原子屈折に3重結合や窒素の補正値を導入する根拠になっているのだろう。
それ以外では、やはり芳香環を持ったものが合わないが、計算値がよく合っている化合物に芳香環を持ったものが無いかというとそんな事も無い。
そこで、まず、ニトリル基について考えてみる。ニトリル基は3重結合を持つ以外に、何か特徴的な分子特性は無いだろうか?
先ほどの篠田耕三先生の書籍では、こうした溶媒は非プロトン性溶媒に分類されるとある。
非プロトン性溶媒、つまり、活性水素を持たず、双極子相互作用やファンデルワールス力が主に働く溶媒である。
特に非共有電子対を持ち、双極子モーメントや誘電率の大きい(15以上)溶媒を、特に非プロトン性極性溶媒(Dipolar aprotic)、もしくは、ドナー性溶媒(Donor Solvent)と呼ぶ。
これらは、会合を起こしやすく沸点が高いとある。
ハロゲン原子の屈折率から考えて、先ほど「ある原子が媒体中に存在すると、ファンデルワールス半径という原子の大きさによって光の速度が変化する」と考えた。
このファンデルワールス相互作用という分子間力が光の速度を変えるなら、双極子相互作用という分子間力も光の速度を変えると考えればニトリルの異常性も説明できるように思える。
また、芳香族は、芳香環の上にπ電子雲を持ち、π-π相互作用という分子間力を持っている。
フッ素で表面を覆われた分子は、フッ素が静電反発を起こすために分子間力が非常に小さく、沸点が低くなる。
そこでこの分子間力を補正項として導入する事によって屈折率の推算式の精度向上を考えてみる事にする。
有機分子の主だった分子間力は、ファンデルワールス相互作用、双極子相互作用、水素結合相互作用、π-π相互作用であろう。
ハンセンの溶解度パラメータは、蒸発のエネルギーを、分散項(Dispersion energy)、分極項(Polar energy)、水素結合項(Hydrogen bonding energy)の3つに分割したものだ。
π-π相互作用は便宜上、水素結合項に入れられている。
(逆に言うと、訳の分からないエネルギーは皆水素結合項に閉じ込められている。)
最近の研究では水素結合項をさらにドナー性とアクセプター性に分割して、4次元のベクトルとして考えている。
HSP値に加え、分子の形状因子もRDに大きな影響を与えている。
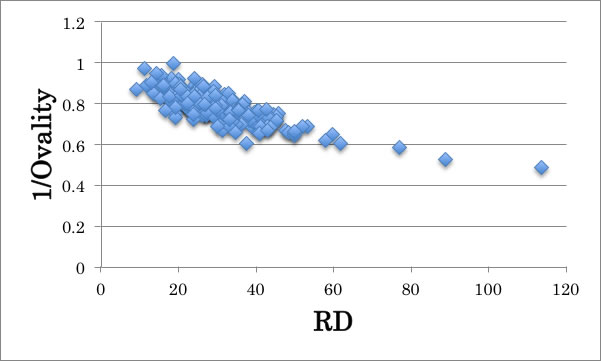
Ovalityは分子の球形度を表す指標で、分子が球形に近づくにつれて1になる。線状分子では2ぐらいになる。
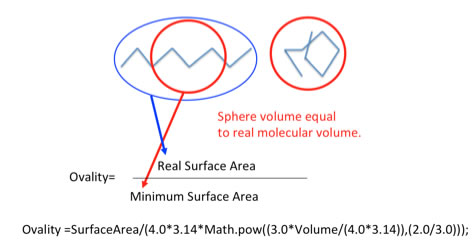
他の指標がすべて同じであっても、球形のものは1/Ovalityが1に近くなり、RDの値は小さくなる。これらの原子の数、HSPと1/Ovalityを使って推算式を構築してみる。
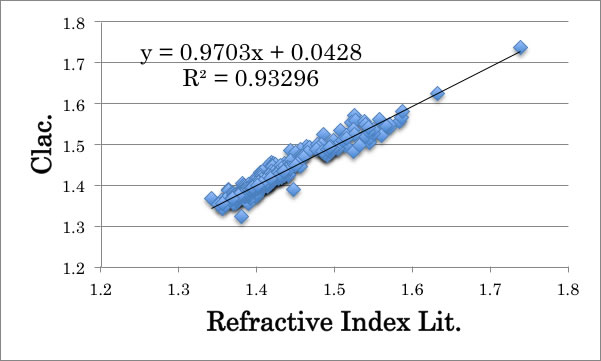
すると、原子の数だけを使った時の、R^2 =0.92039からR^2 =0.93296と改善される。しかし、原子団寄与法で作成した推算式、R^2 =0.97491には及ばない。
そこで、原子の数、HSPと1/Ovalityという入力項同士が相互作用をしていると仮定して、どのような相互作用を考えた時に推算精度が高くなるかを検討する。
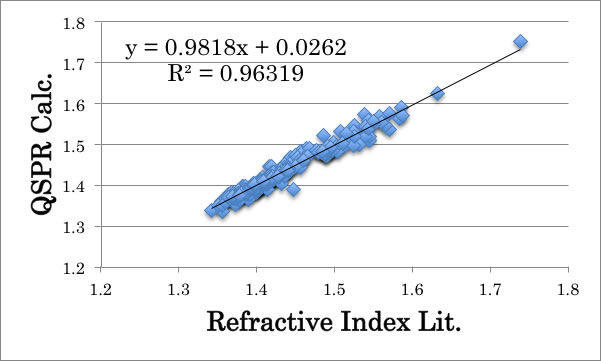
例えば、RDを大きくする相互作用としては、
Hansen dD * N# +1.2082
Hansen dP * S# +1.2108
RDを小さくする相互作用としては
C# * N# -0.8569
Hansen dHac * S# -0.6870
などが見つかり、屈折率自体の推算精度も非常に改善される。
例えば、高屈折率のプラスティックレンズを設計しようと考えた場合、HansenのdP(分極項)の大きいものを使い、かつ、硫黄原子が入ると、屈折率がさらに高くなるが、Hansen dHacも高いと、硫黄の効果は半減するとか言う事が、こうした係数を全て持つ事によって定量的に理解する事が可能になる。
当然の事ではあるが、MVol(分子体積)自体も分子間相互作用の大小によって値が変化するので、MVol自体の高精度な推算式も不可欠である。
また、表面張力(γ)を推算する、Macleod-Sugdenの式がある。
γ0.25 *MW/(D-d) = P (parachor)
D:液体密度、d:気体密度
このパラコルは原子団寄与法で推算する事が可能とされている。このパラコールとRDは下に示すように非常に良好な相関がある事が知られている。
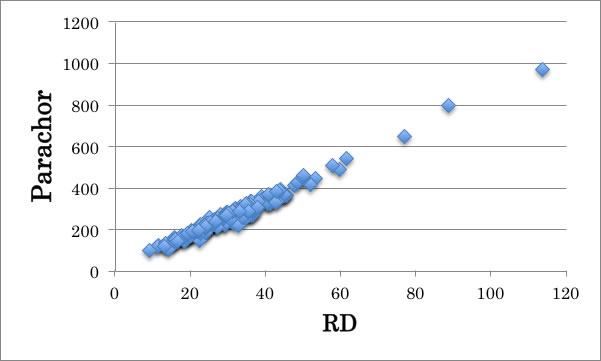
従って屈折率と密度が既知の場合には表面張力を推算する事が可能であることも知られている。
また、RDはもともと体積の次元を持っているが、臨界体積(Vc)とも下図に示すように非常に高い相関を持っている。
臨界体積は対応状態原理(Yen-Woods法)によって密度を推算する上で欠かせない物性値だが、実験値は少ない。RDから屈折率を得るにも密度は必須なのでこの関係は重要である。
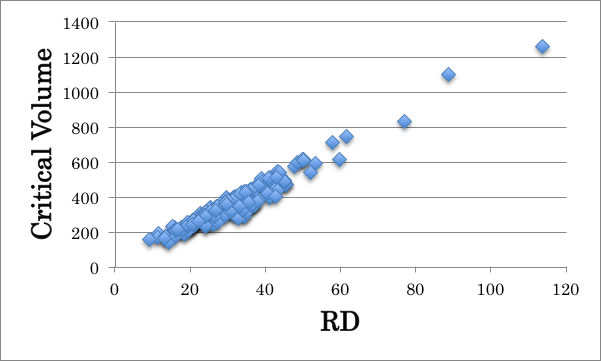
また、臨界圧力(Pc)とも下図のように相関があり、臨界定数が未知の場合屈折率と密度からおおよその値を得るという事がなされている。
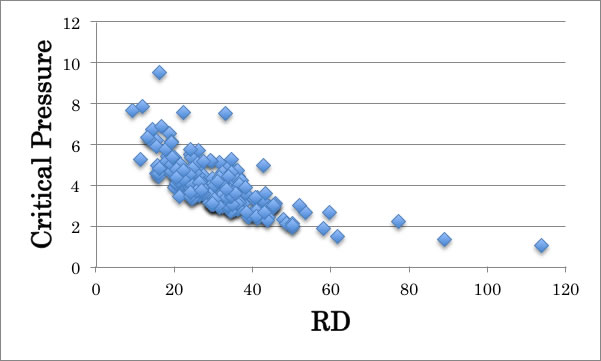
屈折率の温度依存性のデータは、Organic Solventsには120系程度あるが、他のデータ集にはほとんど見かけない。
モル屈折RDが密度の情報を含み、温度依存性をこの密度から補正するため、RD自体は温度依存性が無いと考えられているのでデータ値が無いのだろう。
念のためOrganic Solventsのデータを解析してみる。
HSPiPのY-Predictを用いると、化合物の構造のみから様々な物性値を推算する。その推算された物性値と屈折率の温度依存性(dn/dT)の相関を調べ、最も相関係数が高い物性値を探すと、熱膨張率のパラメータmと高い相関があることが判る。
この熱膨張率は
TEC=a*(1-T/Tc)m
で表される。Tcは臨界温度でaとmは化合物特有のパラメータである。
例えば、チオフェンを例に取り説明すると、温度に対して密度をプロットすると下図のようになる。
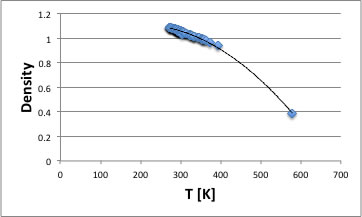
温度の上昇と共に密度は低下し、臨界温度で臨界密度(MW/Vc)に到達する。この曲線の傾きが熱膨張率になる。
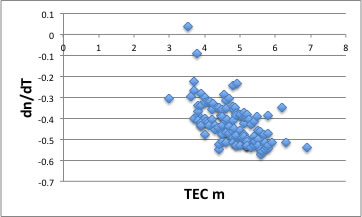
各化合物についてTECのmを求めて、dn/dTに対してプロットすると上図ような相関が得られることがわかる。
熱膨張のしやすさと屈折率の温度依存性が相関があることは、溶媒分子の相互作用が分子屈折と相関が合ったことにも符合し非常に興味深い。
以上のように、RDは他の熱力学的な物性値のファミリーと密接な関係を持った指標であることがお分かりいただけたと思う。
この指標を推算しようとした時に、数多くの原子団に加算値を割り振る原子団寄与法が最も精度が高くなるが、原子屈折に分子間力の指標であるハンセンの溶解度パラメータと分子の形状因子(Ovality)を導入したQSPR式も精度は十分であり、かつ、実際の分子設計に多くの知見を与える式となる事を示せたと思う。
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
