2013.8.16
物性化学トップページ
表面張力の推算法も参照してください。
次世代HSP技術、HSPと表面張力を参照してください。
表面張力(ひょうめんちょうりょく、英語: surface tension)は、表面をできるだけ小さくしようとする傾向を持つ液体の性質、またその力のことで、界面張力の一種である。
正確な定義を言うならば、液体表面の持つ、内部に比べて余剰な単位面積当たりの自由エネルギーである。
液体表面が小さくなろうとするのは、熱力学第二法則よりギブズエネルギーが小さい状態は安定するため、エネルギーの大きい表面分子が小さい内部分子に置き換わろうとするためである。(WikiPedia)
ある液体(炭素数4)があったときに、これらの液体の25℃での表面張力の値によって並び替える事ができるだろうか?
それをしようと思ったとき、化合物のどんな指標を使おうと思うだろうか?
| Hcode | Liquid |
| 92 | n-Butanol |
| 255 | Ehtyl ether |
| 1060 | n-Butylaldehyde |
| 481 | Methyl ethyl ketone |
| 116 | Butyronitrile |
| 114 | n-Butylic acid |
| 328 | Ethyl acetate |
| 285 | N,N-Dimethylacetoamide |
| 260 | Diethyl sulfide |
| 91 | 1-Butanethiol |
| 105 | n-Butyl amine |
| 252 | Diethyl amine |
| 81 | 1,3-Butadiene |
| 1154 | Decafluorobutane |
| 152 | 1-Chlorobutane |
| 3670 | 1-Bromobutane |
我々は油は水に浮く事を知っている。それは、水と油が混じらず、油の比重が水より軽いからである。
しかし、比重が水よりも重い1円玉が表面張力によって水の上に浮かぶ事も知っている。
そして、水は非常に大きな表面張力を持つ事も知っているので、上の表のような化合物があった時に、水溶性の化合物は大きな表面張力を持っていると考えがちである。
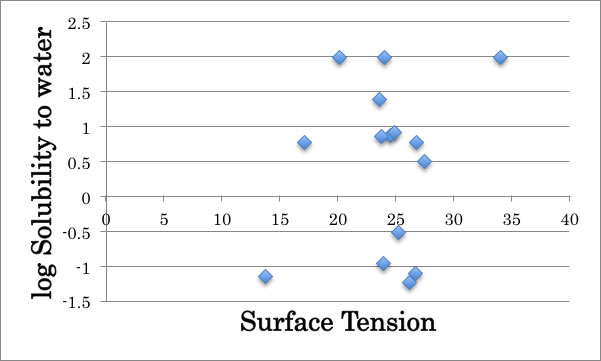
しかし、表面張力と水への溶解度の対数を図示すると上図のようにこの考え方は間違っている事がすぐにわかる。
水への溶解度以外には、ダイポールモーメントや、誘電率から表面張力を並び替えようと考えるかもしれない。
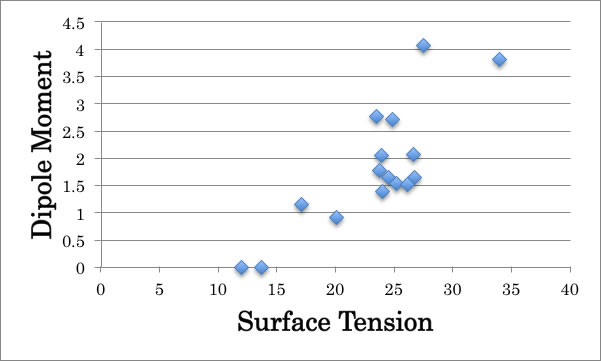
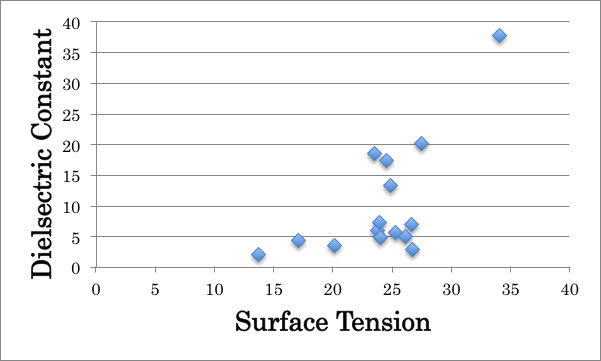
おおまかな傾向は正しいが、順位付けできるほどの精度が無い事もわかる。
そこで、水溶性、ダイポールモーメント、誘電率をごちゃ混ぜにして、“親水性”、“親油性”という曖昧な言葉でお茶を濁す事をする。
“親水性”化合物は表面張力が高く、“親油性”化合物は表面張力が低い。これは正しいのだろうか?
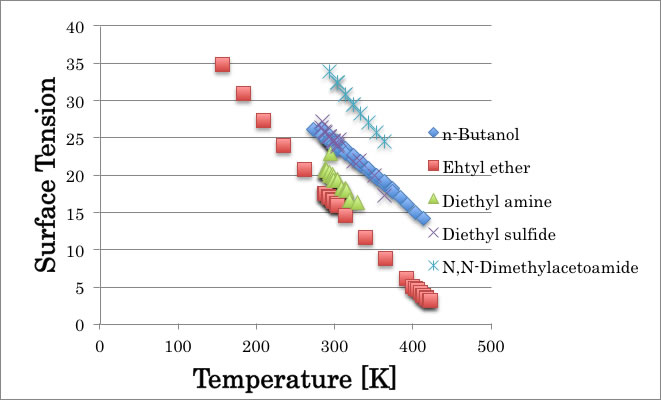
表面張力の温度依存性を図示すると以下のようになり、“親水性”のアミドやアルコールが上にきて、エーテルなどの親油性”化合物が下に来るので正しいようにも見える。
問題は“親水性”、“親油性”という言葉の定義だ。
例えばアミンを親水性の官能基と認めたとしても、ジエチルアミン、ピロリジン、ピロールの表面張力の違いをどうすれば説明できるのだろうか?
| Diethyl amine | Pyrrolidine | Pyrrole |
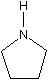 | ||
| γ=20.05 | γ=29.65 | γ=37.6 |
鎖状のNHと比べ、環状のNHは親水性が高く、二重結合の隣にあるNHは更に親水性が高い。
いったい幾つのNHを定義したら全てのNHを表す事ができるのだろうか?
表面張力の推算式として最も著名なMacleod-Sudgen式では、Sudgenは実際に次のようなパラコールを定義している。
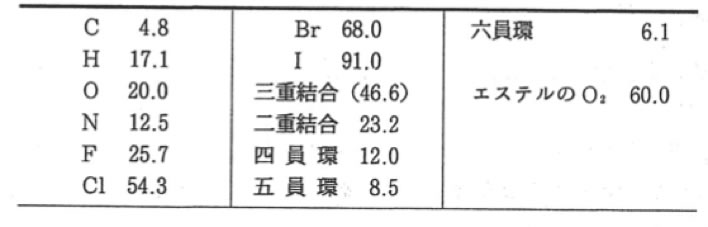
(井本稔、表面張力の理解のために、高分子刊行会、1993)
環や2重結合に補正値を入れないと推算式の精度が上がらない事は、1924年のSudgenの論文の時から認識されている。
| Ehtyl ether | Tetrahydrofuran | Furan | |
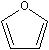 | |||
| γ=17.06 | γ=27.2 | γ=24.1 | |
| Diethyl sulfide | Tetrahydrothiophene | Thiophene | |
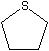 | 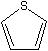 | ||
| γ=25.2 | γ=35.8 | γ=32.8 | |
ところが、エーテル酸素やチオエーテルでは、環状になる効果は同じだが、2重結合の効果はアミンとは同じではない。
さらに、分子の形状の効果もある。
n-Butanol | 2-Butanol | i-Butanol | t-Butanol |
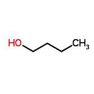 | 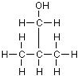 | 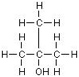 | |
| γ=24.52 | γ=23 | γ=23 | γ= 19.56 |
分子が球形に近づくにつれ、表面張力は低下する。
Beerbower (1971) は表面張力の推算に下式を提案している。
γ=0.0715*MVol1/3 [dD2 +0.632*(dP2 + dH2 )]
dD, dP, dHはハンセンの溶解度パラメータ。
蛇足ではあるが、自分はハンセン先生と溶解度パラメータの仕事をしている。
今年(2013)デンマークのハンセン先生のご自宅で様々な打ち合わせを行った際、ハンセン先生から教えていただいたのだが、自分(Hansen先生)はこの溶解度パラメータをハンセンの溶解度パラメータと呼んだ事は無い。ハンセンの溶解度パラメータ:HSPというのはBeerbower教授が名付けたのだと。
ちなみに前出の井本稔先生の書籍では、BeerbowerがBeerwoberになっているが、間違いである。
この式を評価してみたところ、分子がある程度大きい場合には、非常に精度よく推算できている事が判った。しかし、この式をC4の化合物に適用したところ特にアルコールで大きな誤差になってしまう事も明らかになった。
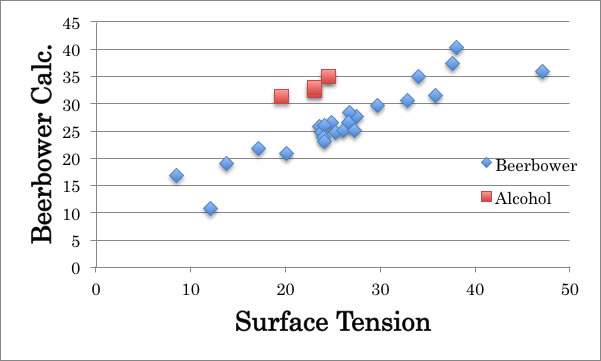
それにしても、表面張力を見積もる指標として、最も優れているのハンセンの溶解度パラメータ(HSP)であると言える。アルコール類の異常は水素結合によるものと考えるかもしれないが、n-butylic acidは例外にならないので水素結合によるものではない。
HSPのおおもとのエネルギーは蒸発潜熱(Hv)である。
Total HSP = SQRT ((Hv-RT)/MVol)
(R: ガス定数, MVol: 分子体積)
蒸発潜熱の実測では、沸点における測定が最も安定(常圧では沸点では温度が変化しない)であるので、沸点における蒸発潜熱の値が最も精度が高い。しかし、HSPでは25℃における蒸発潜熱が必要になる。そこでWatson式を使って沸点における蒸発潜熱を25℃に変換する。
dHv2=dHv1((1-Tr2)/(1-Tr1))0.375
(dHv1: 沸点における蒸発潜熱, Tr1 : 沸点 / 臨界温度, Tr2 : 任意の温度 / 臨界温度 )
そこで、沸点における蒸発潜熱、沸点、臨界温度が判れば、任意の温度での蒸発潜熱が計算できる。
この式の指数、0.375 はどこから来たのだろうか?
この式の精度は?
どのような化合物に適用できる/できない?
これについては説明しておいた方がいいだろう。
たとえば、いくつかの化合物について、温度に対する蒸発潜熱をプロットすると下図のようになる。
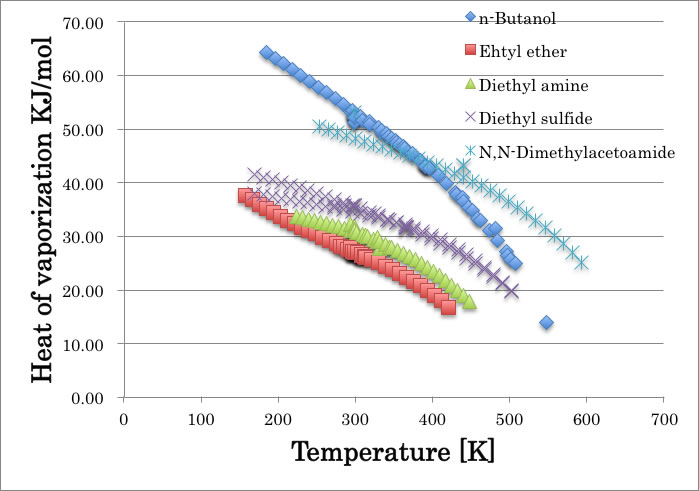
曲線は化合物ごとに異なる。例えば、n-Butanolでは、温度が上昇するにつれて水素結合が切断されて急激に蒸発潜熱が小さくなる。他の曲線は大体、平行関係にある。そして臨界点では蒸発潜熱は0になる。
Watson 式の言っている事は、この図のX軸を温度から、(1-T/Tc)に変えなさいということだ。
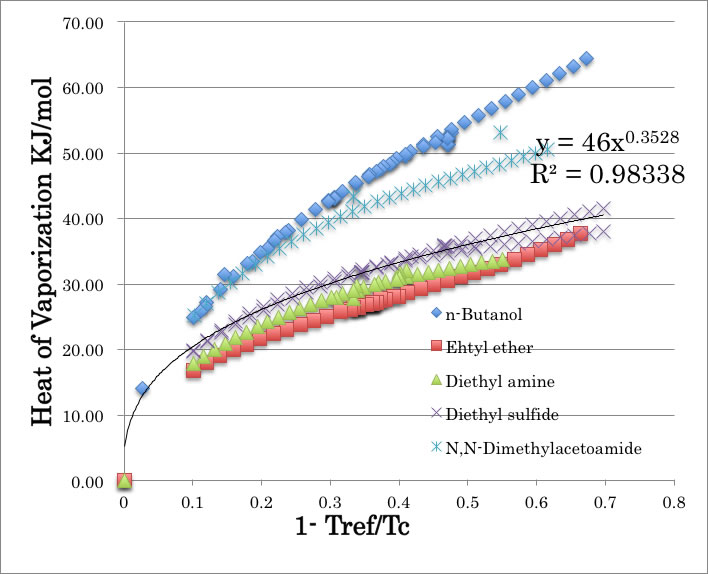
すると原点では蒸発潜熱は全ての化合物で0になるので、式の一般化が可能になる。
そうすると、水素結合性の化合物は大きく外れるがそれ以外の化合物の曲線はほぼ一定になる。
試しにdiethyl sulfideの曲線をカーブ・フィットすると指数の係数は0.3528になる。
つまり、Watson式の指数は、化合物ごとの指数を平均すると0.375になると言っている事になる。従ってWatson式は水素結合性の化合物には使えない。
表面張力も臨界点では0になる。そこで、Watson式と同様、X軸を(1-Tref/Tc)へ変更するのは有効だ。

X軸を変更すると下図のようになる。
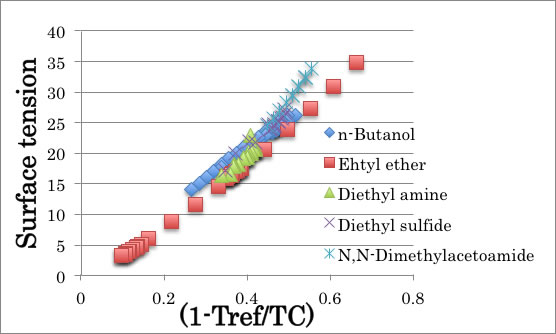
蒸発潜熱の場合と異なり、表面張力では水素結合性の化合物でも曲線はほとんど完全に一致する。
この事は何を意味するかというと、液体の表面張力はTc(臨界温度)のみによって決まっているという事だ。
表面張力が高いというのは、測定温度(25℃)がTcから遠くはなれているだけの事だ。
フロンなどのフッ素系の溶媒が表面張力が低いのは臨界温度が室温に近いだけの事だ。
親水性”、“親油性”も水素結合も全く関係ない!
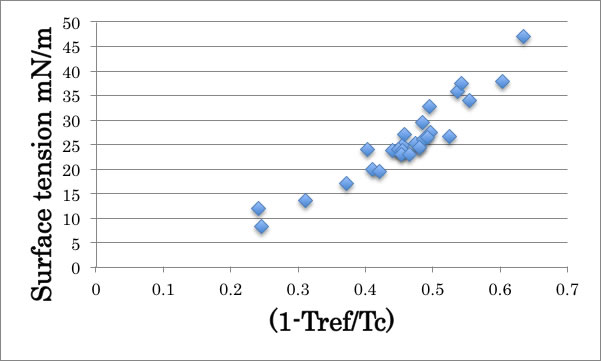
C4化合物の表面張力を(1-Tref/Tc)に対してプロットすると上図のようにきれいな相関が得られる。
原子ごとの効果がキャンセルされたので、分子の形状因子の効果を見てみる。
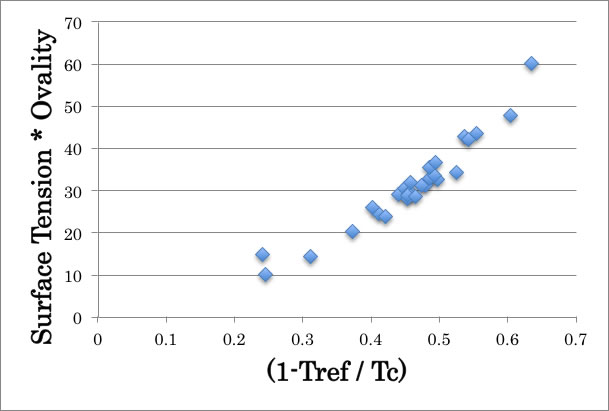
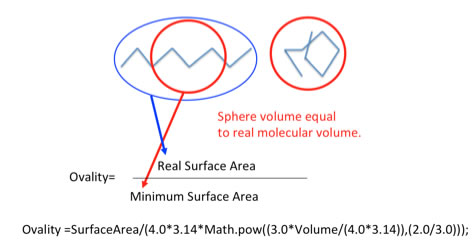
表面張力にOvalityをかけてあげると、さらに精度が上がる事が上図から判る。
Beerbower の論文には (1971), さらに面白い式が書かれている。
d (ln γ)/dT = -4.0 * α
α: Thermal expansivity
この式は Macleod – Sudgen 式から導出される。
γ= (P*(ρ-d)/M)4
P: parachor, ρ: density of liquid, d: density of Gas, M: molecular weight
ここで気体の密度を0とすると次のように変形できる。
γ= (P/V)4
lnγ= 4ln(P) – 4ln(V)
もし、Parachorが温度依存性の無い物性値であるなら、式の温度微分は次のようになる。
d (ln γ)/dT = -4.0 * d ln(V)/dT
表面張力の温度微分は分子体積の温度微分と相関があることになる。こうした関係はマランゴニ数を推算する場合に表面張力の温度微分が必要なので重要な式であると言える。
上式で温度を使うと分子ごとに異なってしまうので、(1 – Tref/Tc)を使い,この式の妥当性を検証した。
γ = 82.106* X1.5069
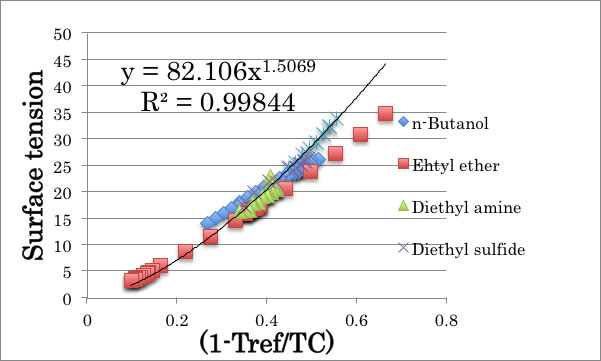
同様に、分子体積の式を作ると次のようになる。
Volume = 77.82 * X-0.221
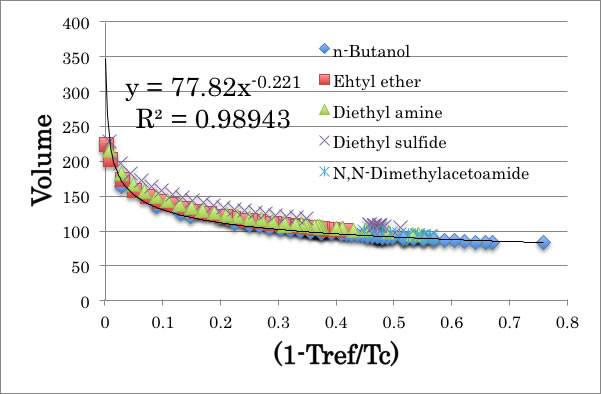
Xの前の係数、82.106と77.82はほぼ同じなので、2つの式から次式が得られる。
ln γ = -7.0 * ln Volume + Const.
この式を検証する。
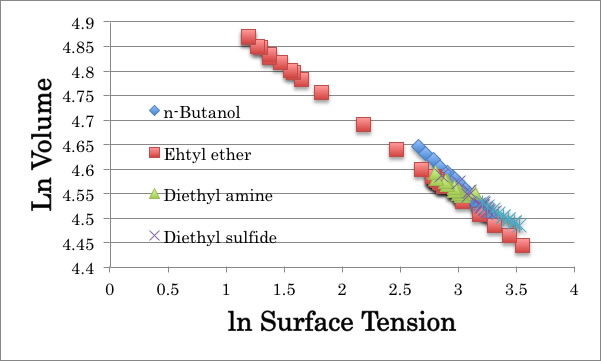
すると、上図のようにきれいに直線に乗る事が判る。
現在、HSPの温度依存性は、熱膨張率から算出される。
d/dT δD = -1.25α δD
d/dT δP = – α δP/2
d/dT δH = -(1.22 x 10-3 + α/2)δH
α = a*(1-T/Tc)m
次元が異なるので、この式は正しくないと思っていたが、表面張力や溶解度パラメータの温度微分は、分子体積の温度微分=熱膨張係数と関係があると考える根拠が、このBeerbowerの式になる。
これらの知見を基に、表面張力をハンセン・タイプに分割するQSPR式を構築してみた。
Butyronitrile の例では下図のようなる。
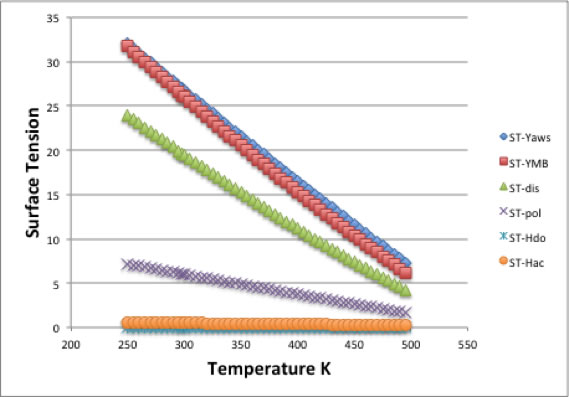
n-Butanol の例では次のようになる。
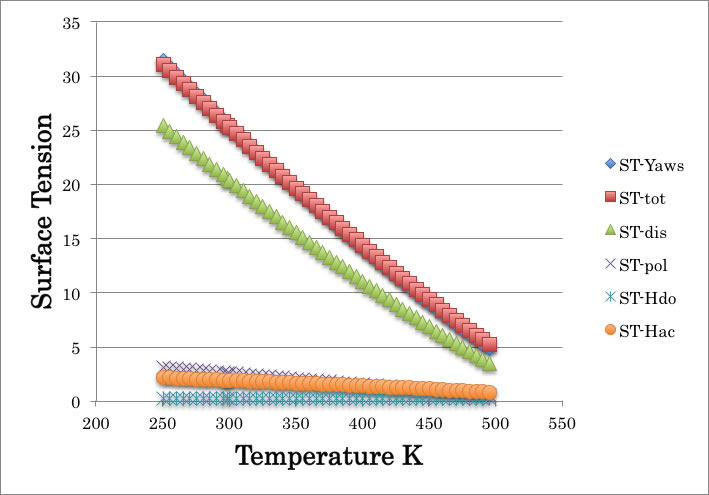
緑色: ST-dis, 分散項
紫: ST-pol, 分極項
水色: ST-hdo, 水素結合、ドナー性
オレンジ: ST-hac, 水素結合、アクセプター性
全表面張力(赤)はそれらを足したものになる。
ST-tot= ST-dis + ST-pol + ST-hdo + ST-hac
表面張力の水素結合項はアルコールであっても非常に小さくなる。これは親水性”、“親油性”も水素結合も表面張力には関係ないので当たり前かもしれないが、ハンセンの溶解度パラメータとは大きな違いである。
この表面張力の4次元分割ルーチン、新規計算方法については、将来はHSPiPに搭載されるかもしれない。(先にどうしても使いたい場合には、HSPiPユーザーであればURLをお教えしますので連絡をいただければと思います。)
ちなみに Macleod – Sudgen のパラコールの値はモル屈折[RD]と相関がある。
γ= (P*(ρ-d)/M)4
P: parachor, ρ: density of liquid, d: density of Gas, M: molecular weight
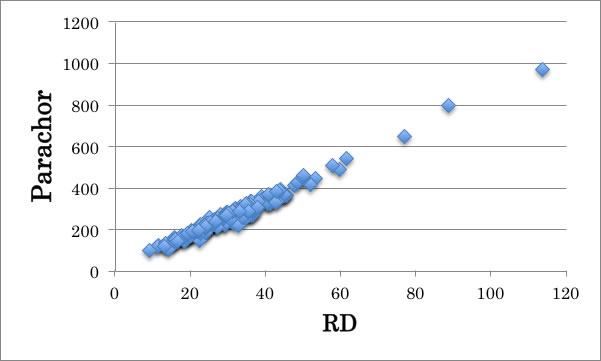
詳しいことは屈折率の推算その2を参照して頂きたい。
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
