2024.9.27
物性化学トップページ
Pirikaで提供するプログラム
2011-2024年横浜国大(YNU)で行なった授業で使ったYNU-YMBを公開した。
重原子は15まで、CHNO以外の原子は1以下。パラメータは2013年のものなので古い。JSMEの使い方はこちらを参照して欲しい。
以降、2011.6.23の古い記述。
HTML5制限バージョン(統合化バージョン 2011.6.13)
(Pass Codeがない場合、重原子は8つまで。S, F, Clは使えない)
iPhone/ipod Touchをお使いの方はこちらのプログラムを試して頂きたい。(マウスではタッチイベントが発生しないので分子が描けない)
その他のバージョン
YMBシミュレータ(HTML5 プログラム 2011.6.10 Pass Codeを持っているならこちらの方が精度は高く、温度依存性も計算する。)
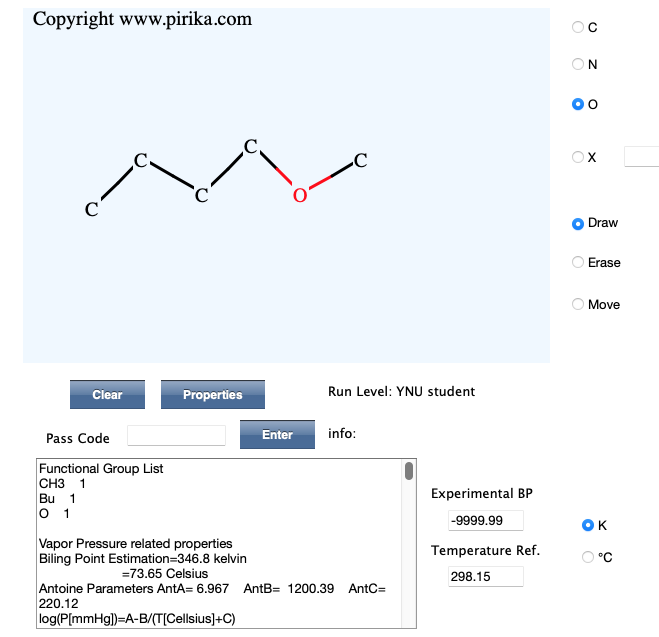
蒸気圧の温度依存性
最新の推算方法は、HSPiPに搭載されている。HSPiPに搭載の商用版では、F, Cl, Br, I,S, P, B, Siが使える。芳香族も扱え、最大重原子数は120になる。
プログラムによってどんな原子団が使えるかはこちらで確認のこと
沸騰の科学についてまとめた。こちらから参照して欲しい。蒸気圧に関して理解が深まると思う。
定義:
蒸気圧とは:一定の温度において液相または固相と平衡にある蒸気相の圧力。
蒸気張力ともいう。
一般に飽和蒸気圧(2相が熱平衡にあるときの圧)を意味することが多い。
固相と平衡にある蒸気相については昇華圧ともよばれる。
1成分2相系の熱平衡において温度と蒸気圧との関係はクラウジウス-クラペイロンの式(1850年)として知られている。
実用的な経験式として、ランキン-デュプレの蒸気圧式がある。
すなわち、飽和蒸気圧pと温度Tとの関係は、式
log P = -A/T + B – C log T
でよく近似される。Tは絶対温度、Aは物質の気化熱に関する定数、BおよびCは気体および凝集系(液体または固体)の比熱に関する定数である。
クラウジウス-クラペイロンの式:物質の2つの相、例えばある液体とその蒸気が熱平衡にある場合の圧力をp、絶対温度をTとし、また第1の相の比体積をv1、第2の相の比体積をv2とし、さらに温度Tで単位質量あたりの第1の相から第2の相への転移熱をΔhとしたとき、次の関係をいう。
Δh=T(dp/dT)(V2-V1)
この式ははじめクラペイロンが熱を物質と考える熱素説の立場から導き、のちにクラウジウスが熱力学の法則から正しく導いた。
Δh=T(dp/dT)(V2-V1)を
dp/dT= ΔHv/TΔVb=ΔHv/(RT2/p)ΔZb
と変形する。
ΔHv:蒸発熱 ΔVb:蒸発による体積の変化
ΔZb:Z(gas)-Z(liq) Z:圧縮率(=pV/RT)
ΔHv/ RΔZbが温度によらないと近似して上式を積分すると
Ln P = A – B / T B = ΔHv/ RΔZb
これが、Clapeyron式になる。
実験値からA,B の定数は最小2乗法を用いれば容易に求まる。
Antoine式(1888年)はClapeyron式がΔHv/R ΔZv が温度によらないという仮定からのずれを補正した式で、
log( Pvp) = A – B / ( T + C ) であらわされる。
左辺が自然対数Lnであったり、Tを絶対温度でとったり、℃でとったりで定数のA,B,Cの値が異なっている。
左辺がlogで温度を絶対温度でとったとき、経験的には
C = -18 + 0.19 Tnbp
とあらわせるとある。
岩波書店 岩波講座 現代化学15 化学と情報
大木道則、佐々木慎一、千原秀昭 遍
C=0の時はClapeyron式に戻ってしまう。
有機化合物の蒸気圧を信頼性高く推算する事は、環境に放出される化合物の影響評価を行う上で非常に重要である。
例えば、CFCやHFCが漏れでた場合、蒸発速度、オゾン破壊係数、地球温暖化係数などを推算するためにおおよその蒸気圧を知る必要がある。
蒸気圧の推算式、相関式は文献上も数多く存在するが、一般的に言ってそれらの式は次の物性値を必要とする。
推算値を使う場合にはこちらを参照してほしい。
(1) 臨界温度, Tc
(2) 臨界圧力, Pc
(3) 蒸発潜熱, dHv か
(4) ある温度での蒸気圧を最低1点。
著名な推算式は次のものである。
Riedel
Frost-Kalkwarf-Thodos
Riedel-Plank-Miller
Thek-Stiel
Lee-Kesler
推算式
Riedel式は次式を使って蒸気圧を推算する。

Tc : Critical Temperature
Pc : Critical Pressure
Tbr : boiling Point / Critical Temperature
Tr = measure Temperature / Critical Temperature
この式に、(Tb,760mmHg), (Tc, Pc)を入れるとぴったり一致する。
また、αcが3.758になる点はQが0になるのでA,B,Dが0になり、Cは3.758になる。この点も必ず通る。
このように、常にこの3点を通る曲線を与えるのがRiedel式だ。
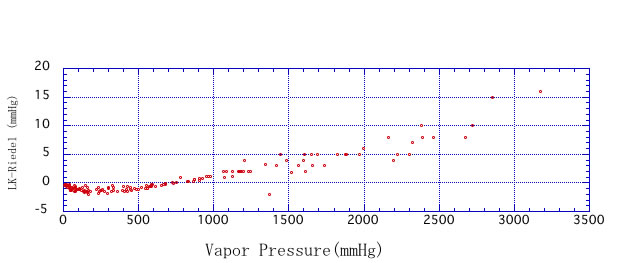
Cが3.758になるのは沸点以上なので、高圧の領域で精度が高くなる方法だ。”The properties of Gases & Liquids”に臨界定数と沸点、Antoine定数のある化合物について、この方法の精度を検証したのが下の図だ。
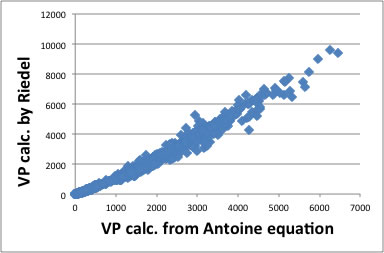
乱数で、Antoineの温度範囲で適当な温度を発生させて、antoineの蒸気圧とRiedelの蒸気圧を計算してプロットしてみた。(この場合はAntoineの蒸気圧式が正しいと仮定している。)
意外と蒸気圧が低いほうが精度が高いように思える。
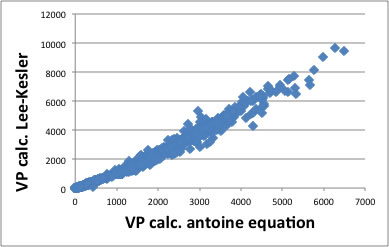
Lee-Kesler法は次式で蒸気圧を推算する。Riedel法と同じく対応状態原理法の一つだ。

ωは偏心因子と呼ばれる。
式の形から明らかなように、ωの上辺の式はf(0)と-ln(Pc)と符号が違うだけで同じ形、下辺はf(1)と同じ形になる。
そこでTmes(測定温度)にTbを入れるとTrはθとおなじになり、右辺は-ln(Pc)だけが残る。
この場合の蒸気圧はatm単位なので、LnPは0,つまり1atmになる。(つまり常に(Tb,760mmHg)を通る。)TmesにTcを入れるとTrは1になる。
それをf(0)(Tr)に入れると7e-5, f(1)(Tr)に入れると7e-6になる。
ωは2以下なので右辺はe-4程度、つまり圧力はPcになり、やはり臨界点を通ることになる。同様に精度を検証するとRiedel法とほとんど同じになった。
このαcとωをプロットしてみると、ほぼ完全に一致する事がわかる。
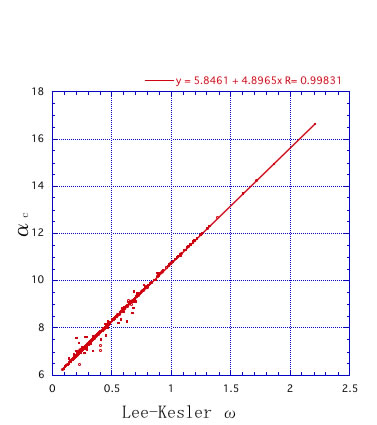
そこで、この二つの式は、形は異なるが同じパーフォマンスを持つと予測される。
事実、化合物ごとにどのくらいの差が出るか調べてみると、推算値はほぼ完全に一致していることがわかる。
対応状態原理を使った蒸気圧式は他にもあるが、沸点と臨界点を必ず通るようにパラメータを決めるので、結果はどれも似通ったものになる。

自分もニューラルネットワークを使って、蒸気圧を推算する式を構築して、PirikaのHPに載せてある。
この場合は、沸点や臨界点を通るという制限が無い分、(実験値の)データを検証すると精度は低めに出てしまう。
しかし、臨界点や沸点が推算値の場合、Reidel式やLee-Kesler式はその推算値を通る答えを出すが、NN法はそうした制限が無い分、予測値は精度が高くなる。
多くの場合、臨界点がもとまっているような化合物は蒸気圧が求まっていて、Antoine式などにフィッティングされている。
問題になるのは臨界点が求まっていない、高沸点の化合物の蒸気圧をどう推算するかだ。
従って、推算値の沸点、臨界点を必ず通ってしまうというのは、実は好ましいことではない。
YNUーシミュレータでは蒸気圧は分子構造から直接Antoine定数を推算してしまっている。それは新しいAntoineパラメータのフィティング法を開発し、アントワン定数の安定性が飛躍的に向上したからそれが可能になった。
また合わせて臨界点の推算法も改良されているので、こうした対応状態原理法もまた違った結果になっているかもしれない。
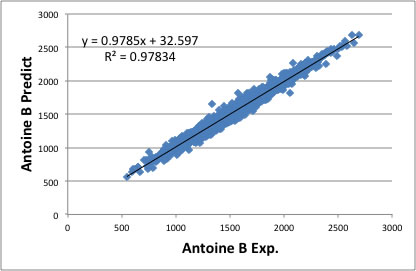
HSPiPに搭載したAntoineのBを推算する時の精度は下のようになる。167種類の官能基について、新規に定めた2178化合物のAntoine定数を解析した結果だ。
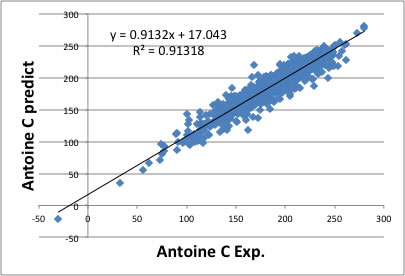
同様にAntoineのCの精度は以下のようになる
残念ながらAntoineのAパラメータは構造からは推定できない。(2023, 最新版ではAntoine Aも分子構造から推算する)
そこで、沸点の実験値(ない場合には推算値の沸点)を使ってAパラメータを定める方法がHSPiPのYMBに搭載されている。
実験値が一つでもあれば(Antoine のAを実験値から定めれば)精度は非常に高い。
例えば、シックハウス原因物質の25℃での蒸気圧を文献値のAntoine式から求めたものと、沸点のデータがあるものはそれを、無いものは沸点の推算値を使って25℃での蒸気圧を計算した(VP-YMB)を比較すると下のようになる。
| 厚生労働省による濃度指針値のある物質 | BP | VP@25 | VP-YMB |
| アセトアルデヒド | 294 | 899.91 | 890.21 |
| トルエン | 383.78 | 28.40 | 23.90 |
| キシレン | 417.58 | 6.64 | 7.46 |
| エチルベンゼン | 409.35 | 9.48 | 7.81 |
| スチレン | 418.31 | 6.18 | 6.00 |
| パラジクロロベンゼン | 447.21 | 1.79 | 1.45 |
| クロルピリホス | 320F (Decomposes) | 9.22E-11 | |
| テトラデカン | 526.727 | 0.010046424 | 0.014587166 |
| フタル酸ジ-n-ブチル | 613.15 | 8.40E-07 | 9.43E-07 |
| フタル酸ジ-2-エチルヘキシル | 657.15 | 1.95E-15 | |
| ダイアジノン | 0.000993785 | ||
| フェノブカルブ | 0.000715988 | ||
| 文献値Antoineから | YMB-Antoineから |
ほぼ満足できる結果であるがどうだろうか?(ただし、HSPiPのバージョンによっても値は変わる。小数点以下の丸め込みの精度から、この結果と完全に一致することはない。)
2012年横浜国大講義資料:塗る太陽電池の設計で、Antoine定数を使った材料設計を紹介した。基礎物性の推算方法が応用科学にどう使われるか、参照にして頂きたい。
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
