2022.9.16改訂(2010.7.26)
解析例トップ
HSP応用トップページ
概要
対応状態原理（Law of Corresponding State）を使うと様々な熱力学物性を化合物に特有のパラメータを使うこと無く推算できる。
何故それが可能になるかというと、臨界点（臨界温度、臨界圧力、臨界体積）を使った還元値を使うと推算式がこの還元値だけで表すことができるためだ。
HSPも同様で、HSPベクトルを比較できるのは、HSPの原点は蒸発潜熱がゼロになる臨界点であるからに違いない。
対応状態原理(Law of Corresponding State)
van del Waalsの 状態方程式 (P + a/v^2 )(v – b)=RT
a: 分子間に働く弱い引力
b: 体積の除外項
この式に臨界点 (Tc, Pc, Vc) を入れると
a=3PcVc^2 , b=Vc/3 と求まる
VDW方程式は
(Pr + 3/Vr^2 )(Vr – 1/3)=(8/3)Tr
と書く事ができるが、この式には分子固有のパラメータ、a,bが含まれない。
（とは言っても沸点や臨界値は分子固有のパラメータであるが）
（Pr=P/Pc, Vr=V/Vc, Tr=T/Tc 還元値と呼ぶ）
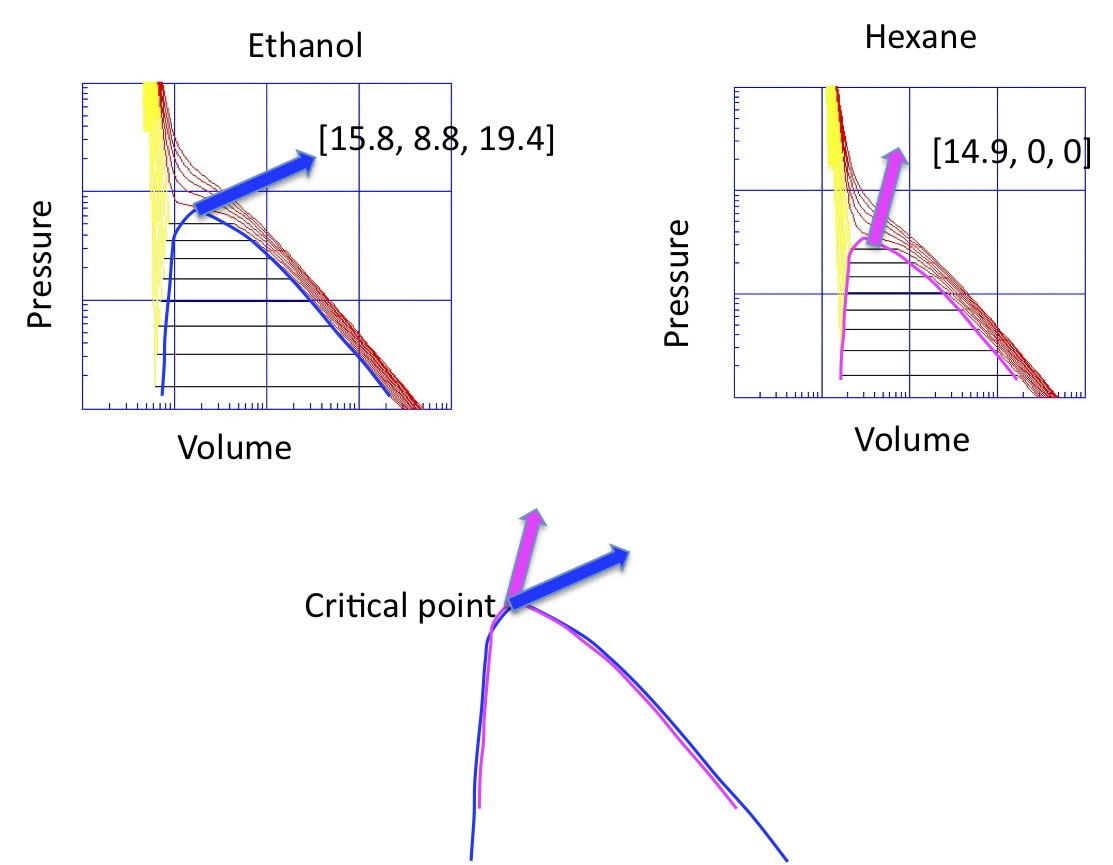
これを図で表すと下のようなる。
エタノールとヘキサンは、PVTの図の絶対値は異なるが、臨界軌跡(気液共存の両端を繋いだもの)は一致する。
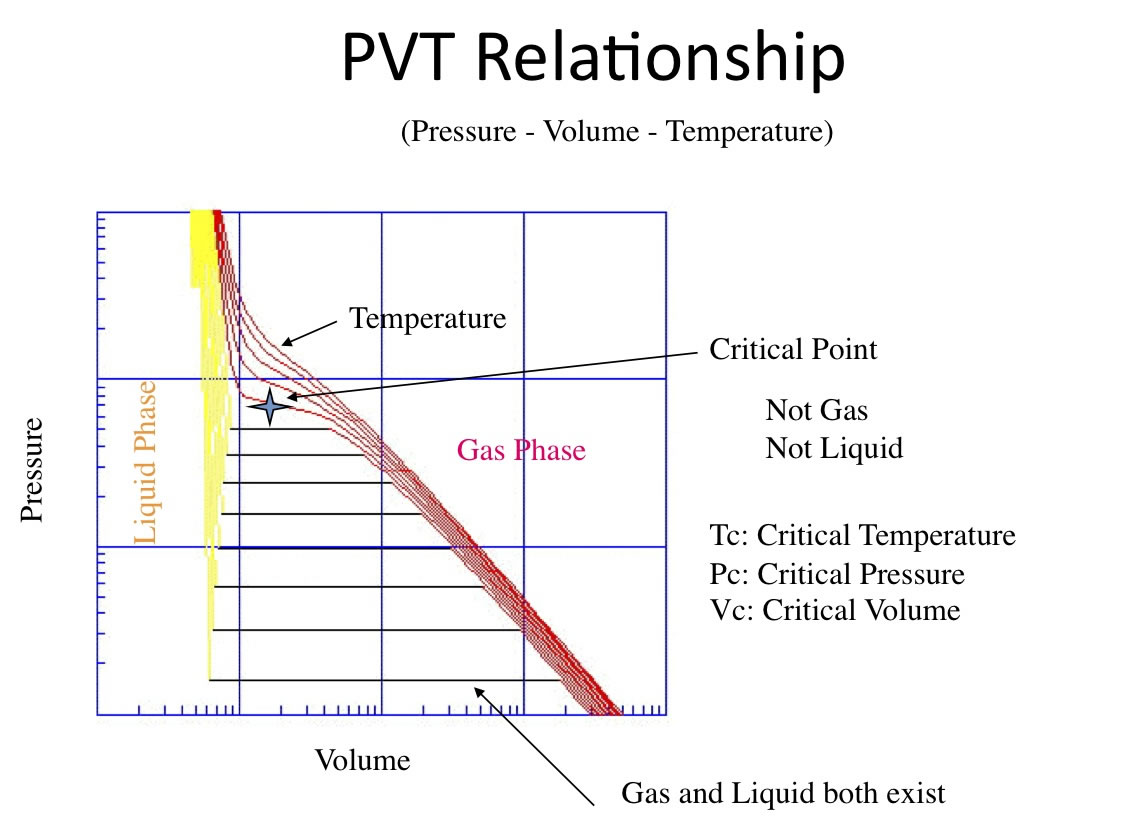
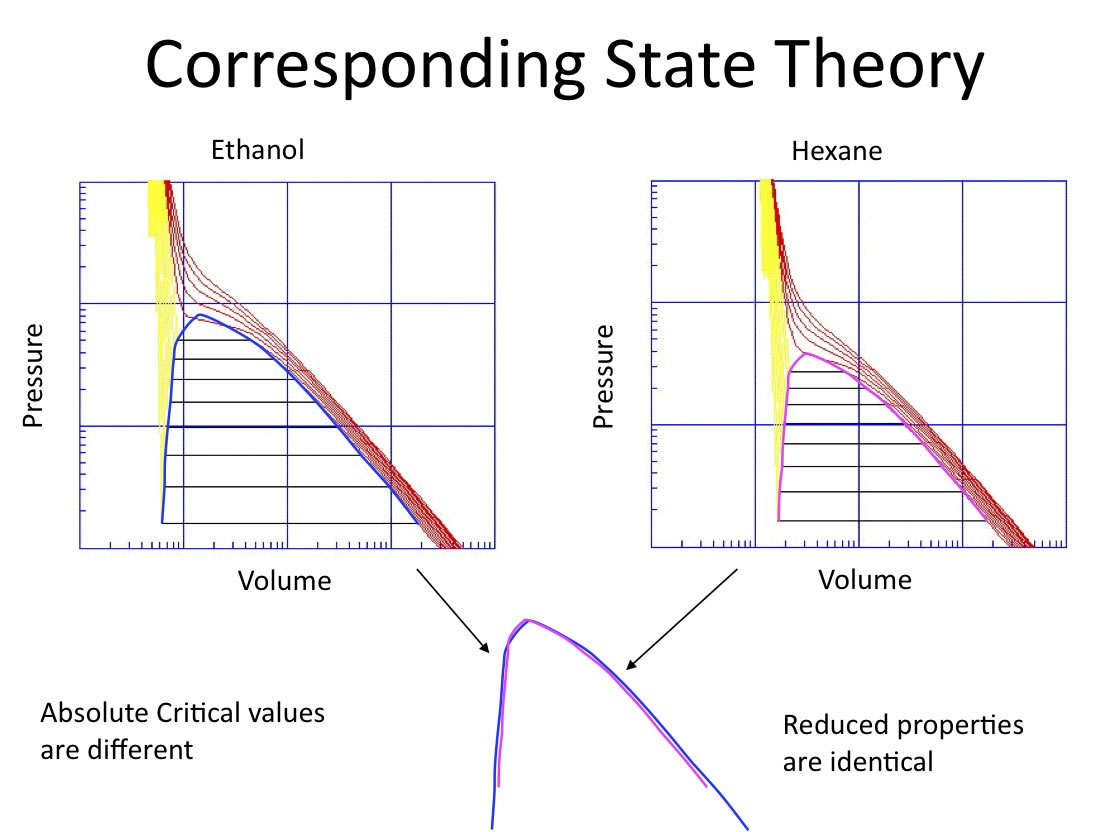
| Tc:514K Pc:6.137MPa Vc:168cm^3 | Tc:507.6K Pc:3.059MPa Vc:371cm^3 |
このように、臨界値と還元値があれば、熱力学的な物性値の多くは推算することができる。
推算は一つの式、臨界値からの相対距離で表す事ができる。
沸点と臨界点の値があるのであればpirikaのこちらのページで実際に計算してみよう。
沸点と臨界点はHSPiPとSMILESの構造式があればY-MBで計算もできる。
例えば蒸気圧は下のような式で推算する事ができる。
Ex. 蒸気圧の推算
(Tc, Pc) と(Tb, 1気圧）を通るという条件がつく。
Ln ( P / Pc ) = h (1 – 1 / Tr )
h = Tbr * ln(Pc) / (1-Tbr)
P: 蒸気圧
Pc: 臨界圧力
Tc: 臨界温度
Tr: 測定温度 / 臨界温度 (還元温度と呼ぶ)
Tbr: 沸点/ 臨界温度
P/Pc : 還元圧力
このように、臨界点と沸点を使うことによって、どんな化合物であっても同じ式で蒸気圧を表すことができる。
下に示すような、多くの推算式が構築されている。
従って物性推算にとっては臨界点、沸点の情報は非常に重要である。
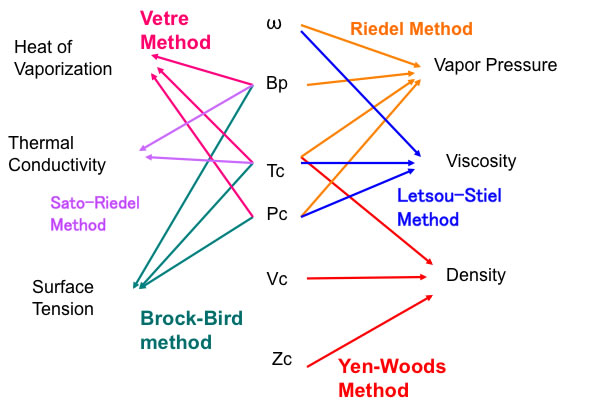
Pirikaで紹介しているの沸点と臨界点を用いた対応状態原理法による物性推算
| 蒸気圧 | Riedel Method |
| 蒸発潜熱 | Pitzer-Carruth-Kobayashi method |
| 熱伝導度 | Pirika Neural Network method |
| 粘度 | Pirika Neural Network method |
| 表面張力 | Pirika Neural Network method |
| 密度 | Yen-Woods |
しかし、沸点や臨界値の物性値はほとんど増えていない。
有名なデータベース、Dipper 801を調べてみると、臨界温度で、沸点の1/3、臨界圧力では1/4程度の実験値しかない。
| Experimental data | Predicted data | Unknown source | |
| Boiling point | 1128 | 149 | 35 |
| Critical Temperature | 420 | 850 | 4 |
| Critical Pressure | 324 | 953 | 4 |
| Critical Volume | 269 | 1011 | 9 |
測定が高温になる事、高温では分子の分解が問題になる事から、臨界点の実験値がこれ以上増える事は期待できない。
沸点や臨界定数の推算法
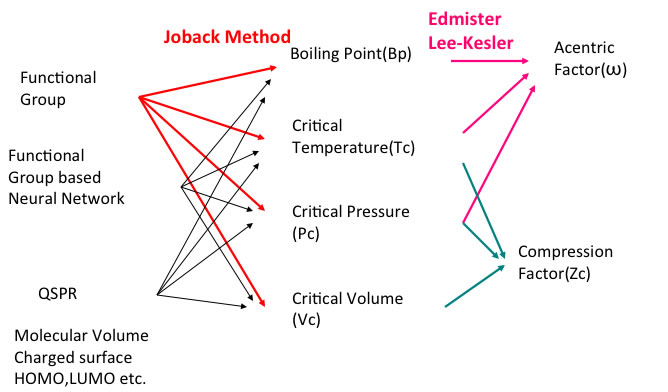
様々な物性推算式が構築されているが、実は沸点の推算すら容易ではない。
pirikaの沸点推算
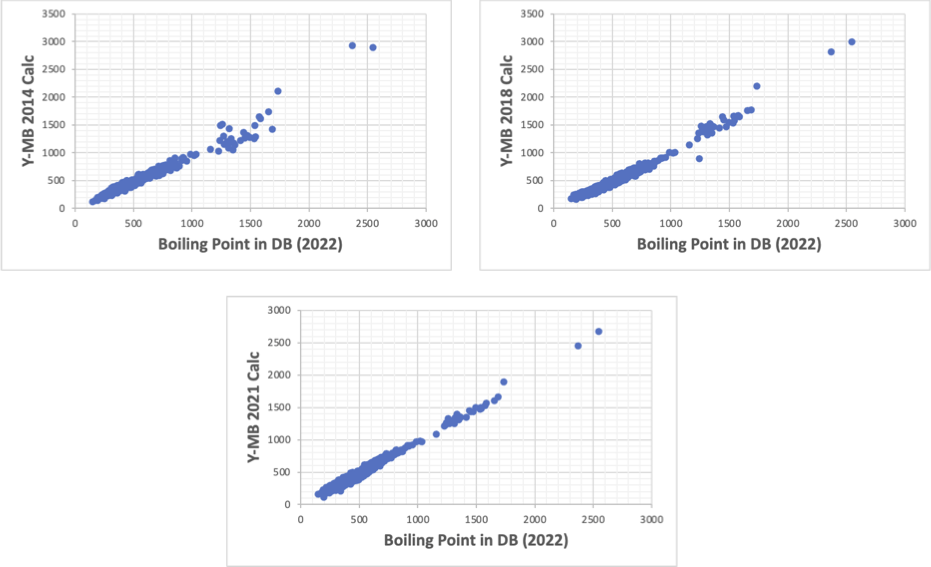
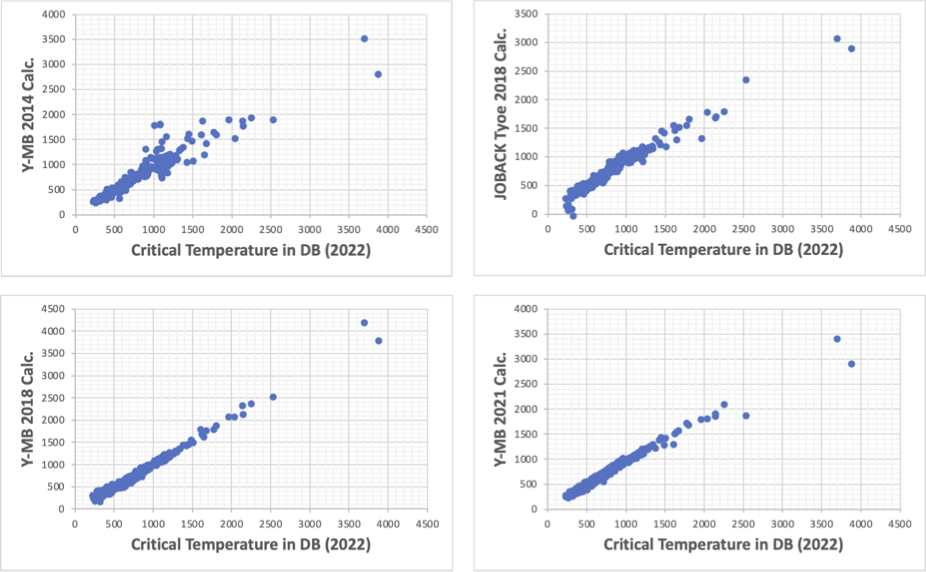
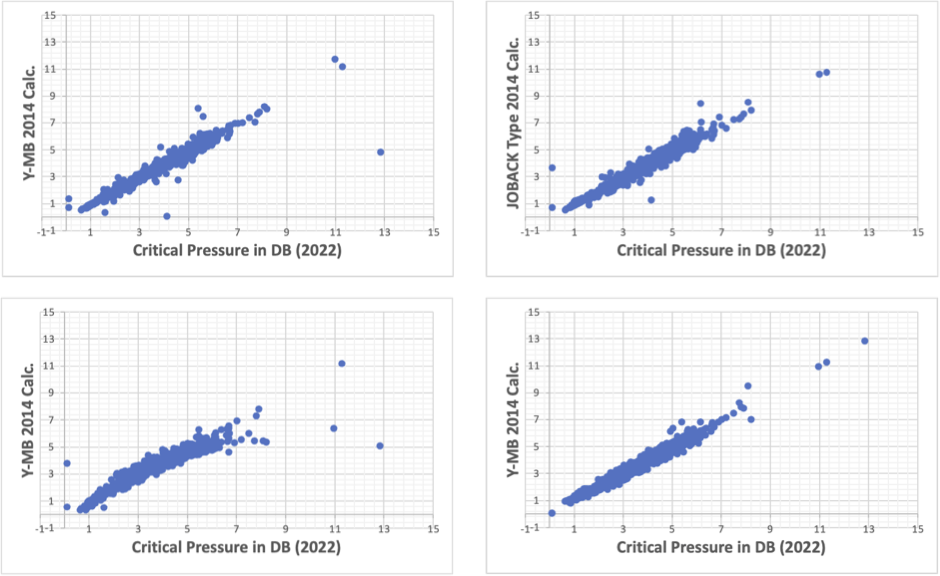
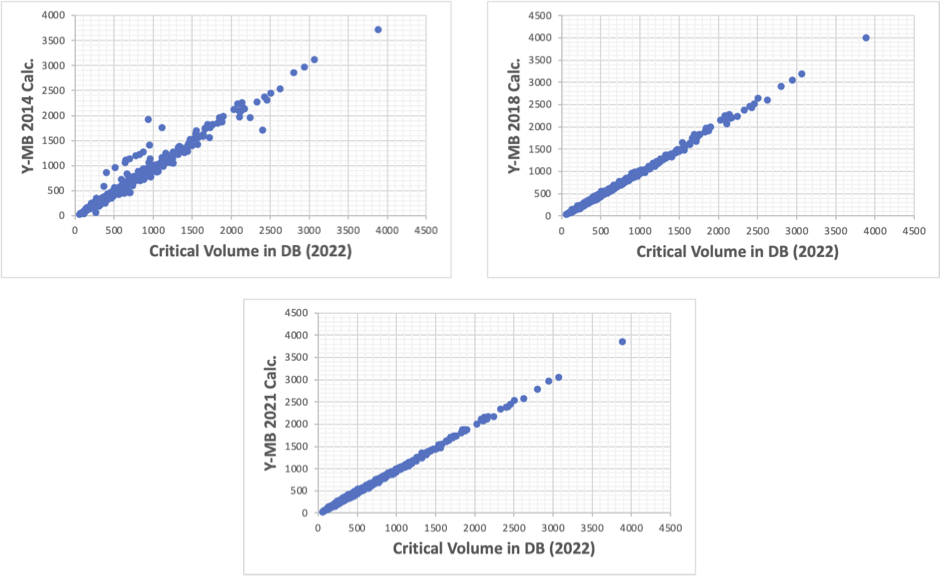
ところで、ハンセンの溶解度パラメータは熱力学的な物性値であるのに、臨界点を使わずに溶解度を推算している。
その理論のベースになる蒸発潜熱は、Vetre法、Riedel法とも対応状態原理であるので臨界点を使う。何故、臨界点がいらないのかハンセン先生と議論になった。
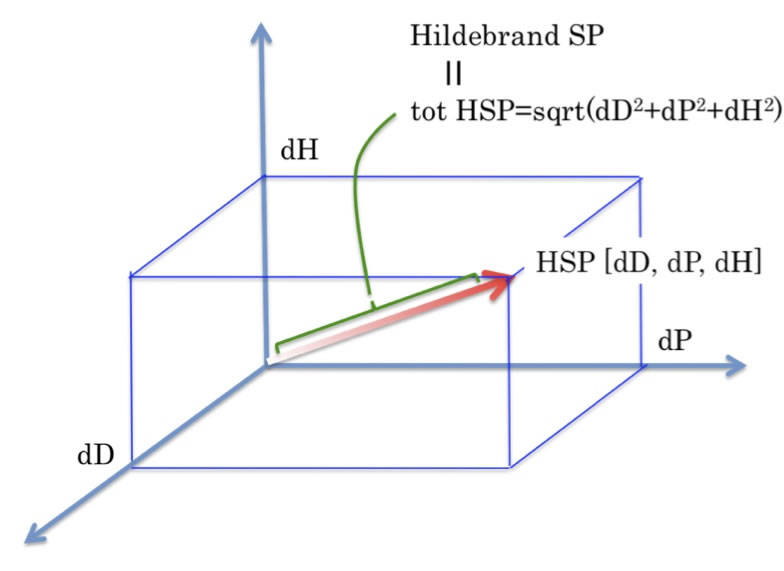
先生との結論は、ハンセンの溶解度パラメータは蒸発潜熱をベースにしている。
そして蒸発潜熱は臨界点でゼロになる。
従って、上の図に示す、ハンセン空間の原点は臨界点となる。
（臨界点ではベクトルの長さがゼロになる）
そこで、我々は各々のベクトルを同次元で比べる事ができるのではないかという結論に達した。
イメージで表せば、下図のようになる。
臨界点はこれ以上増えないが、HSPは質の高いデータがどんどん集積されている。
HSPiPには、可能な限りの臨界点、熱力学物性値を収集している。
またPirikaで構築した物性推算式も搭載ししている。
それらを利用するには、化合物のSmilesの構造式を準備して、Y-MB機能を使って推算するだけでよい。
YMBを使った熱力学的物性値の推算に関しては、フランスの CNRS(Center National Research Science)が非常に興味を持っている。Abbott先生と訪問した。
解析例トップ
HSP応用トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください