2022.9.25
解析例トップ
次世代HSP^2
その他トップページ
これは、pirikaのブログに2021.12.23に投稿されたものです。
LUMiSizerは無機物の分散評価を行う装置としては非常に優れている。今回、その装置を用いると得られるデータが入手できたので、少し解析を行ってみた。
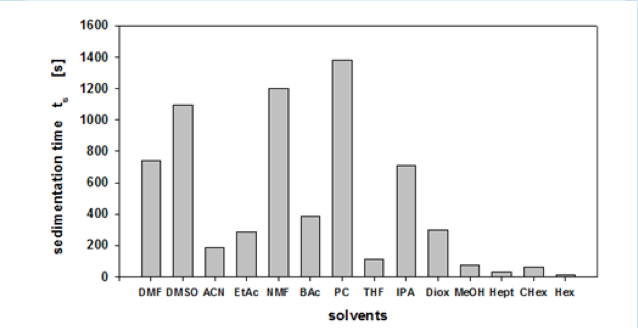
この装置を使うと、例えばある顔料を14種類の溶媒に対して分散させたものから、Sedimentation time(沈降時間)が得られる。ある溶媒では、すぐに沈降するのであるが、ある溶媒では沈降が遅くなる。そして、それを相対沈降時間(RST)にして（どうやって？）、RST norm >0.5を良溶媒、<0.5を貧溶媒として、HSPiPで解析を行うと、顔料のHSPとハンセンの溶解球が得られると記載してある。
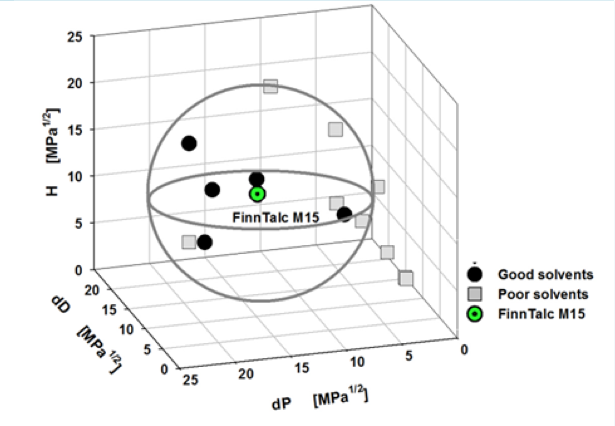
これは、今までのHSPの標準的な使い方だし、書いてあることが間違いだとは言わない。
でも、HSP2を使うともっともっとHSPが豊かにる。
ドイツの、Lerche先生には来日した時にお会いして、それを説明したのだが、あまりちゃんと伝わっていなかったようだ。
例えば、溶媒のED(Electron Donar)とEA(Electron Acceptor)の値は、塩基性顔料、酸性顔料の分散を評価する時には必須になる。dHacid, dHbaseも重要だ。HSP2ではdDもdDvdwとdDfgに分割している。つまり、1つの溶媒に対して、７種類のパラメータがあることになる。
この計算方法はまだHSPiPに搭載されていないので、今回使ったデータはコピーしてエクセルなどに貼り付けて使って欲しい。
このように次元数が高くなってしまうと、これまでのハンセンの溶解球のように3次元表示できなくなるのが最大の問題だ。
そこで、今回は主成分分析(PCA)法を用いて次元圧縮する方法を試してみよう。
PCA法は、軸(Axis)を変換(Transformation)するのでAXになる。
これまでに、
CX(Chemical Transformation)
BX(Bio Transformation)と来たので、今度はAXだ。
主成分分析(PCA)
日本の訪問者はpirikaのPCAのページも合わせて参照して頂きたい。
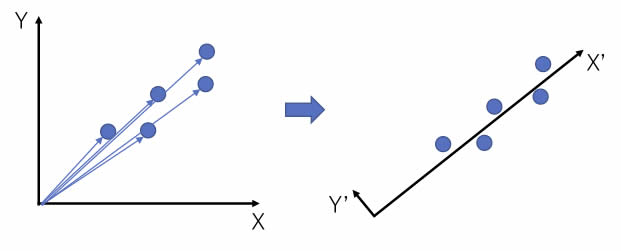
例えば、左の図では2次元のベクトルが5つある。
ベクトルの大きさは異なるが、向きは非常に似ている。
そこで、X軸、Y軸を回転してあげると右のようになる。
X’軸はだいたい元のベクトルの大きさとなり、Y’軸は非常に小さな値になる。 Y’の値が十分小さければ、軸の回転によって2次元ベクトルを1次元ベクトルに下げたことになる。
このように、まずベクトルの一番大きな傾向を第一主成分、それに直交する軸を第二主成分のように取っていく。
このように書くと簡単に見えることも、いざやってみようと思うと、どうやったらいいか全くわからないだろう。
大丈夫！。今の時代、意味不明でもデータのセットの仕方を学べば、後はボタンポチでPCAなど計算してくれる。統計やら解析などはAIとの親和性が高いので、そのうちデータ・サイエンティストなど必要なくなる。
データセットと結果の受け取り方を学ぼう！。
いきなり7次元のデータを解析するのは大変なのでカラムを二つ選んでみる。
どのような列を選ぶかと言えば、沈降速度との相関が高そうなものを選んでみよう。
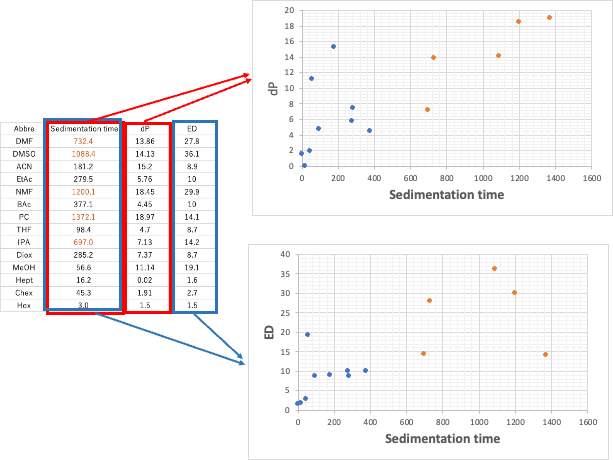
先程作成したエクセルのテーブルに新しいTabを付け加えて、一列目にAbbre、２列目に沈降時間、３列目にdP,４列目にEDを抜き出したテーブルを作成してグラフを書いてみよう。沈降速度が500以上のものをオレンジ色で示してある。
このグラフから明らかなように、沈降速度はそれぞれ、dP, EDと高い相関がある。また、2-3点の例外はあるけど、沈降速度が大きい溶媒は、dP, EDが大きい事がわかる。
そこで、dP, EDの関係をグラフに書いてみると、下図左のように高い相関がある。
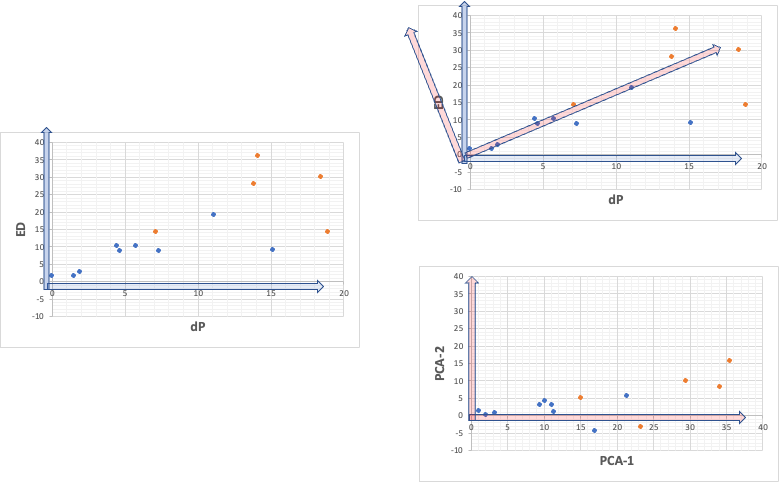
つまり、各点を表す[dP, ED]ベクトルは、大きさはともかく、向きはよく似ていることになる。そこで右上の新しい赤い軸が求まれば良いことになる。右下の図のように、この場合は、第二主成分も最大15ぐらいの値を持ってしまう。
さー、グジャグジャ説明はとにかく、ポチしよう。
新しいタブが開かれるので、ReadDataとしてCalc.PCAとすると、答えが帰ってくる。
この結果から、第一主成分だけでは86.99%しか表現できていない事がわかる。
そして大事なのが、Calculate Schemeの式だ。この式をコピーして、エクセルの適当な列の２行目に=符号をつけてペーストする。（何故２行目なのかは、２行目のC列、D列を参照する式になっているからだ。）これが新しい軸のX座標になる。
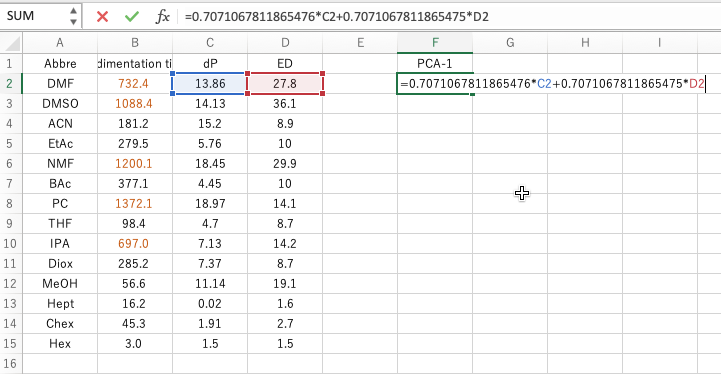
同じように2番目の式を貼り付ける。これが新しい軸のY座標になる。これをプロットすると右下の図が得られる。
これがわかれば、後は、7次元のデータに適用するだけだ。これを第３主成分まで考慮に入れると、92%まで表現できている。
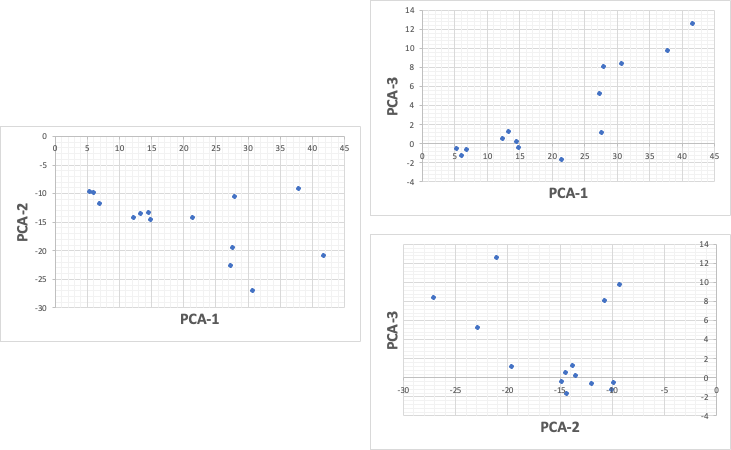
とは言っても、この三枚のグラフから、3次元の位置を頭の中で構築するは無理だろう。
plotly.jsを使うと簡単に３次元表示できる。
これが、HSP2での新しいハンセン空間になる。
オレンジで表示される溶媒を全て球の内側に含むハンセン2溶解球を求めれば、その球の内側に入る溶媒は、皆、沈降速度が500以上であると予測される。
このハンセンの溶解球や軸には、dHacid, dHbase, ED, EAの値も組み込まれている。
もう少し定量的な解析をするなら、我々が作成した、GROVE解析ツールを使う。
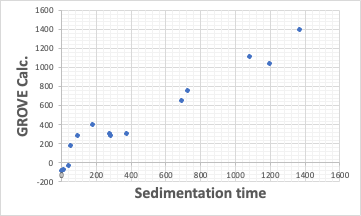
HSP2の7つの変数から重要な変数を３つ選択して、沈降速度の予測式を作成する。
沈降速度=-173.54*dHAcid+13.23*ED+75.12*EA+-109.98
となる。４変数を選択するなら、さらにdDvdwが選ばれる。
つまり、この顔料の沈降速度は、dHAcid（水素結合酸性項)、ED（電子供与性）、EA(電子受容性）に大きく依存していることになる。それは定性的にはPCAの軸への貢献度を見ればわかる。
この事を無視して、古い3次元HSPだけから予測した、「さらに分散性を高める溶媒」は、重要度が低い可能性がある事を覚えておくと良い。
pirikaのDXはこのように、解釈を豊かにすることを目指している。
ちなみに、このブログを読んだAbbott先生は、PCA-Sphereの概念をとても気に入ってくれて、HSPiP ver.6に組み込む事を決定した。古いやり方をしたい研究者はそのまま、ラジオボタンを選択したらPCA-Sphereと切り替えられるようにする予定だ。
解析例トップ
次世代HSP^2
その他トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください