2022.9.10改訂(2010.7.15)
解析例トップ
HSP基礎トップページ
概要
定量性ある「Sphereの中心」の意味について新たに解説を加えました。2023.4.24
新しい距離の33式で定量的な解析を行なった。次世代HSP技術
HSPiPのver. 3.1からはSphereを求めるアルゴリズムに、Dataが加わった。それまでは、”自分の定義する良い溶媒“をScore=1にして、
良くない溶媒をScore=0と定義していた。
これは、定性的な評価であり、より多く溶かすにはどうしたら良いかの指標は与えてくれない。
これを解消するべく、ver. 3.1からは新しいアルゴリズムが搭載された。
古い記述
HSPを決定するプログラム，SphereはHSPiPの中核となるプログラムだ。
様々な成功を収めてきたプログラムであるが，問題点も指摘されるようになった。
そこでVer. 3.1.Xにむけて様々な改良が施された。
最初に、溶解する量を再現できるように、定量的な球を求めるアルゴリズムが搭載された。
この場合のScoreの値は実数が許されている。注意点としては、HSP距離が短いほど、Scoreは大きな値となるように値を入れる。
HPLCのリテンションタイムなどは、逆数にして入力する点だ。
内容
これまでは、”自分の定義する良い溶媒“をScore=1にして、
良くない溶媒をScore=0と定義していた。
この、0と1の境界がハンセンの溶解球（球：Sphere)を構成する。
つまり、HSPiPのSphereプログラムは、ハンセンの溶解球の中心と半径を求めるプログラムになる。
このハンセンの溶解球が求まると、新しい溶媒のHSPベクトルが溶解球の内部に来るか、外部かで溶解性の判断をつけることができる。
ベクトルが溶解球の中に来るときには、”自分の定義する良い溶媒“と同じ程度に溶質を溶解すると言える。
つまり、自分が100g/100ml以上溶けた時を良いとした場合と、
1g/100ml以上で境界を取った場合で、溶解球の半径は大きく変わるし、中心もある程度変わってしまう。
そして何よりも、この方法では量に関しては何も言えない。
つまり、定性的な言い方しかできない。
そこで、より多くの溶質をとかしたい、より分散安定性の高い溶媒を探したいという要望には答え難かった。
そこで、溶解量とHSP距離に相関が出るような新しいSphereの探索アルゴリズムが開発され、HSPiP ver. 3.1以降に搭載された。
私(山本博志）が作ったプログラムではあるが、当初は計算時間が長くかかるとかで、余り使われなかった。10年たってやっと最近評価され始めて来た。
コンピュータがこの10年で非常に早くなったのと、定量的な評価が増えて来たためであろう。
アビエチエン酸の溶解度
実際の例で見て行こう。
Abietic Acid は溶解度が調べられている。
この化合物は、松脂の主成分である。松脂は半田付けに良く利用され、電子基板から松脂を溶解するのにフロン R-113が良く使われた。
オゾン層破壊問題以降、オゾン層を壊さず、地球温暖化に寄与しない溶媒の開発の際にアビエチエン酸の溶解度が検討されたため、データは豊富である。
テーブル
| Name | dD | dP | dH | Vol | g/100CC |
| HCFC-141b | 15.7 | 4 | 1 | 95 | 1.375 |
| HCFC-225cb | 13.1 | 2.9 | 1 | 130.1 | 1.092 |
| carbon tetrachloride | 17.8 | 0 | 0.6 | 97.1 | 5.0688 |
| chloroform | 17.8 | 3.1 | 5.7 | 80.5 | 172.724 |
| dichloromethane | 17 | 7.3 | 7.1 | 64.4 | 123.798 |
| CFC-113 | 14.7 | 1.6 | 0 | 119.2 | 1.2424 |
| tetrachloroethylene | 18.3 | 5.7 | 0 | 102.8 | 115.02 |
| trichloroethylene | 18 | 3.1 | 5.3 | 90.1 | 178.364 |
| 1,1,2-trichloroethane | 18.2 | 5.3 | 6.8 | 92.9 | 64.845 |
| 1,2-dichloroethane | 18 | 7.4 | 4.1 | 79.4 | 43.75 |
| Acetone | 15.5 | 10.4 | 7 | 73.8 | 18.249 |
| methyl ethyl ketone | 16 | 9 | 5.1 | 90.2 | 28.175 |
| diethyl ether | 15.49 | 2.9 | 4.6 | 104.7 | 57.753 |
| toluene | 18 | 1.4 | 2 | 106.6 | 78.897 |
| 1,1,1-trichloroethane | 16.8 | 4.3 | 2 | 99.3 | 94.9696 |
ここでの計算結果は古いもののままだが、生データを提供するので最新版のHSPiPを使って自分でやってみよう。
例えば，溶解度が60g/100CC以上の溶媒のScoreを１として，Classic SphereでHSPを求めて見る。
結果は[18.2, 4.8, 4.4]となる。球の半径は6.15となり，これよりもHSP距離が短い溶媒はScoreが1，つまり良く溶解(60g/100cc)すると判断される。
Abietic AcidをY−MBで原子団に分解し，HSPを推算すると[17.5, 3.1, 6.3]となり，Classic Sphereで計算したものとそれなりに一致する。
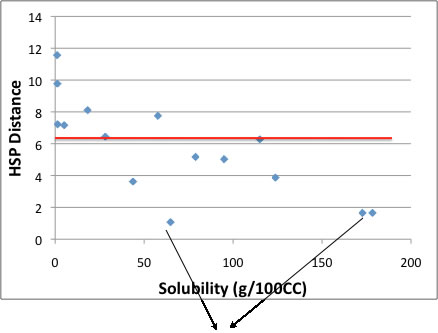
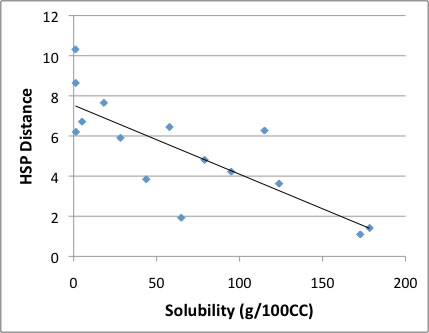
HSP距離は同じなのに溶解度は大きく違う。
この，Classic Sphereの結果をプロットすると上の図のようになる。
HSP距離が6.15より短い時はScoreが1(つまり，60g/100CC以上の溶解度）になる事を示している。
この表現のし方で困るのが，HSP距離と実溶解度に関連が無いことだ。
例えば距離が6.2付近の，Methyl Ethyl Ketone(28.175g/100CC)とTetraChloroEthylene(115.02g/100CC)のように距離が同じでも実溶解度は大きく異なっている。
また，現実問題として困るのが，さらに溶解度の高い溶媒，さらに抽出力の高い溶媒を探したい時に，距離の一番短い（Abietic Acid のHSPに一番近い）1,2-dichloroethaneよりもChloroformやTrichloroethyleneは３倍以上も溶解することだ。
この問題を解決する為に，実溶解度を（平均的に）一番正しく再現できるように球を決定するアルゴリズムを開発した。
Sphere Dataと呼ぶ。
Sphere Dataを使う場合、どこからその機能を使うのか分かりにくい。バージョンによっても名前とか位置が変わる。
Ver5.3の初期では、Advanced Fittingを選ぶとパネルが表示されていた。
Ver.5.3の後期では、Genetic Algorithmという名称になっている。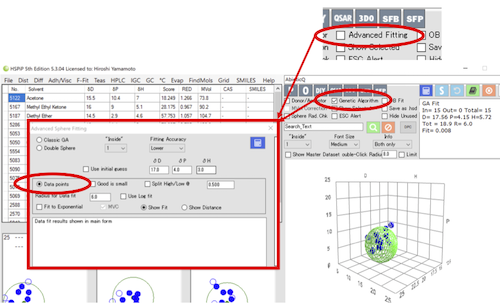
Ver5.4からは２次元図３枚が省略され、そこにSphere計算用のパラメータが集められている。
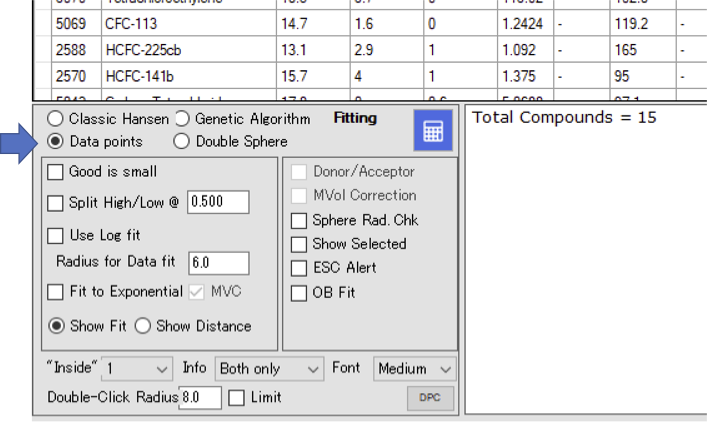
先のデータを使い、メイン・テーブルにデータセットを作れば、すぐに計算できる。
（先生たちはData モードと呼ぶことにしたらしい。非常に解りにくいと自分は思うのだが。）
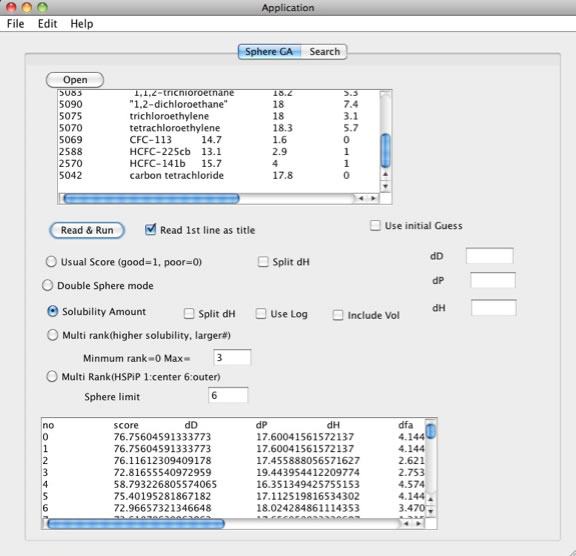
求まったHSPは[17.6, 4.1, 5.9]と、よりY−MBの結果に近い答えになった。
（この計算はver3.1のものだ。最新のHSPiPでやり直してみよう。）
なるべく実溶解度が直線（logを取る事もできる）に乗るように最適なHSPを求める。すると、ChloroformやTrichloroethyleneの近辺に最も多くの量を溶解する溶媒があることが判る。この違いを実際のハンセンの溶解度球で見てみよう。
Drag=回転, Drag+Shift キー=拡大、縮小, Drag+コマンドキーかAltキー=移動。
緑色の大きな球はClassic Sphereで求めたSphere、水色の大きな球は定量的なSphereで、その違いは殆ど無いことが判るだろう。しかしHSP距離と実溶解度は２つのグラフほど異なったものになる。
この例では余り効果が判りにくいかもしれないので，オレイン酸の溶解度の例を示そう。
オレイン酸の溶解度
これは溶解度が30g/100CC以上をScore1として計算を行った。
テーブル
| Hcode | name | dD | dP | dH | ScoreC | ScoreAmount |
| 122 | carbon tetrachloride | 17.8 | 0 | 0.6 | 1 | 107.712 |
| 156 | chloroform | 17.8 | 3.1 | 5.7 | 1 | 136.988 |
| 534 | nitromethane | 15.8 | 18.8 | 5.1 | 0 | 0.6774 |
| 456 | methyl alcohol | 14.7 | 12.3 | 22.3 | 0 | 24.9956 |
| 10 | Acetonitrile | 15.3 | 18 | 6.1 | 0 | 0.8646 |
| 367 | 1,2-dichloroethane | 18 | 7.4 | 4.1 | 1 | 32.625 |
| 7 | Acetone | 15.5 | 10.4 | 7 | 0 | 21.646 |
| 570 | isopropyl alcohol | 15.8 | 6.1 | 16.4 | 1 | 43.175 |
| 481 | methyl ethyl ketone | 16 | 9 | 5.1 | 0 | 26.9675 |
| 328 | ethyl acetate | 15.8 | 5.3 | 7.2 | 1 | 39.688 |
| 92 | butanol | 16 | 5.7 | 15.8 | 1 | 45.765 |
| 255 | diethyl ether | 15.49 | 2.9 | 4.6 | 1 | 42.78 |
| 148 | chlorobenzene | 19 | 4.3 | 2 | 1 | 94.01 |
| 181 | cyclohexane | 16.8 | 0 | 0.2 | 1 | 62.32 |
| 102 | butyl acetate | 15.8 | 3.7 | 6.3 | 1 | 42.336 |
| 417 | hexane | 14.9 | 0 | 0 | 0 | 29.2596 |
| 698 | o-xylene | 17.8 | 1 | 3.1 | 1 | 77.44 |
| 532 | nitroethane | 16 | 15.5 | 4.5 | 0 | 2.2946 |
| 404 | furfural | 18.6 | 14.9 | 7 | 0 | 1.5015 |
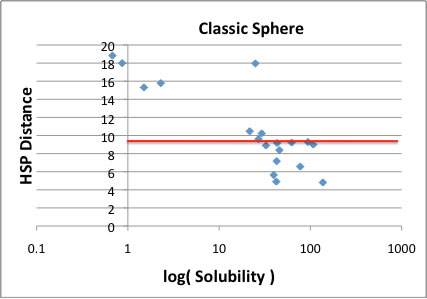
Classic Sphere で計算すると，HSPは[16.9, 0.6, 9.4] 半径9.23になった。
それに対して，Sphere Data で計算すると，[18.7, 1.1, 4.4]になった。
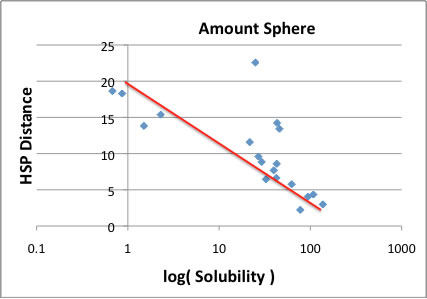
この場合は実溶解度を上げる方向がどちらであるか非常に明確に理解できる。
赤い直線の上の方にずれている３点はアルコールで，それについては別途説明する。
この違いを先ほどと同様に実際のハンセンの溶解度球で見てみよう。
Drag=回転, Drag+Shift キー=拡大、縮小, Drag+コマンドキーかAltキー=移動。
緑色の大きな球はClassic Sphereで求めたSphere、水色の大きな球は定量的なSphereで、今度は随分違うことが判るだろう。
一連の溶媒は水色の球の中心から放射状に伸びている事が回転させてみると判ると思う。それによって、HSP距離と実溶解度に相関が生まれる。
カプサイシンの溶解性
アセトンー水の混合溶媒にカプサイシンがどれだけ溶解するかのデータに対してこの手法を使ってみた。混合溶媒のHSPは通常のベクトルの加算を使う。
実際に下のデータで混合HSPを計算してみよう。
テーブル
¨C12C ¨C13C
| Name | dD | dP | dH | Score(mg) |
| 1 | 18.1 | 17.1 | 16.9 | 0.896 |
| 2 | 17.835788 | 16.419146 | 15.893962 | 2.598 |
| 3 | 17.579272 | 15.758124 | 14.917228 | 6.743 |
| 4 | 17.323692 | 15.099514 | 13.944058 | 9.748 |
| 5 | 17.05961 | 14.418995 | 12.938515 | 13.241 |
| 6 | 16.804316 | 13.761122 | 11.966434 | 16.49 |
| 7 | 16.541924 | 13.084958 | 10.967326 | 17.378 |
| 8 | 16.288164 | 12.431038 | 10.001086 | 17.94 |
| 9 | 16.026344 | 11.756348 | 9.004156 | 17.687 |
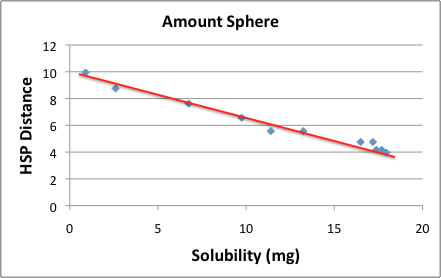
Sphere Dataで計算して、求まったHSPは[17.9, 13.1, 7.8]となる。
この計算値から計算されるHSP距離と実溶解度をプロットすると非常に綺麗な関係だった。
Y-MBの推算値が，[18, 10.5, 12.8]であるので，dHの値が大きく変わってしまっている。この値を用いてHSP距離を計算する。下の図と比べて見ると実溶解度を理解する上ではSphere dataは非常に判りやすい手法であると言える。
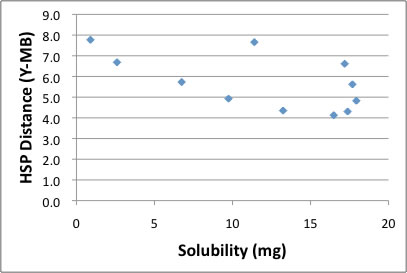
さらに初期値を工夫するなどして，Y−MBの結果にも近く，かつ，実溶解度を再現できるように現在，改良が進められている。
また，この方法は，Sphereの半径の概念が無くなった。
Scoreは実溶解度で連続値なので，0,1で区切られる境が無くなる為である。
大まかには、よく溶解する溶媒の上位1/3ぐらいのところに球を描くと今までの実感と合うようである。
この方法は、溶解度を定性的に扱う(Classic Sphere)か、定量的に扱う(Sphere Data)かの違いなので受け入れやすいと思う。
この機能は、HSPiPのver. 3.1以降に搭載された。GAオプションを選択すると利用できる。
2012.1.9
様々な現象に定量的な解を求めようとする時には、この方法でも十分ではないだろう。全ての現象が溶解度パラメータだけで決まる訳ではない。
そうした取り扱いを自分でやってみよう(DIY)で解説した。抽出蒸留の溶媒の探索、超臨界CO2抽出などではHSPの３成分が全部効いている訳では無い。自分で係数を定めた方がいい事も多々あるだろう。
解析例トップ
HSP基礎トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください