2023.4.24
Sphere(ハンセンの溶解球）探索のオプションData points
このData PointsオプションはHSPiP ver.3.1から搭載されているが、使い方と意味がわからないとの指摘が多い。使い方などの例題はこちらにまとめてある。
ここでは、概念的な説明を行う。
これまで、HSPの理論では、溶質のHSPは次のように決定されてきた。
- HSPが既知の溶媒を使って、ある溶質を溶解試験をする。
- 各溶媒をハンセン空間（分散項、δD軸が約2倍拡張された空間）と呼ばれる3次元空間にプロットする。
- 実験者が定める良溶媒、貧溶媒の定義に従い、各溶媒を色分けする。（良溶媒を青、貧溶媒を赤）
- 青い溶媒はハンセン空間の中である領域に集まっている。
- この領域はハンセンの溶解球と呼ばれ、その球の半径は相互作用半径と呼ばれる。
- このハンセンの溶解球の中心が溶質のHSPと定義される。
これを図示すると以下の様になる。
ここまでは、HSPの基礎中の基礎の話だ。
間違った説明？
これまでの説明（Data Points オプションが搭載されていない、ver.3.1, 2010.12.10以前の話)では、より高い溶解性を求めるのであればハンセンの溶解球の中心、溶質のHSPと同じ溶媒が溶解性が最も高いとされてきた。
その考え方には合理性はある。
例えば、先ほどの溶解実験で、良溶媒と貧溶媒の尺度を少し厳しくしたとしよう。
ハンセンの溶解球は少し小さくなり、これまで良溶媒と呼んでいたものは溶解球の外側へ配置される。
それを繰り返していくと、溶解球の中心のものが一番最後まで残るだろう。
だから、一番よく溶かす溶媒は溶質のHSPと同じHSPを持つ溶媒になる。
しかし、この説明は明らかに間違っている。
溶解性の判断は、良溶媒が”1″,貧溶媒が”0″と定義されているので、定性的な判断になる。一番多く溶解する溶媒はどれであるかは判断がつかない。それはある意味しょうがないことでもある。
溶解に関する定量的なデータ（例えば溶媒への溶解度）を正確に測定する手間と、例えば10gのポリマーを100ccの溶媒へ放り込み、振盪機にセットするのでは大きく違う。
実用的なニーズ
難溶性のものを何とか定性的で良いから溶かす溶媒を探索したいというニーズはそれなりにはあるが、より多く溶かしたという定量的なニーズも多い。
そのニーズに応えるために、sphereの探索オプションにData Pointsが付け加えられた。
しかし、これまでにあまり使われて来なかった。
きちんと概念を説明していないのが悪いのかと思う。
Sphereの概念の拡張
もし、Sphereを輪切りにしたときに、Sphereの中心が玉ねぎの中心にあるのであれば、定性的なSphereで十分かもしれない。
この時の年輪の境は定義した良溶媒と貧溶媒の境だ。
ところが中には中心がずれているものがある。中には中心が２つあるものもある。
特に中心がずれている時に、どうしたらずれた中心の位置を見つけることができるか？というのが問題になる。
これを決めるには、「実際にxg/100g溶媒溶けた」とか「X%膨潤した」「機械強度の劣化がx％だった」、「粘度が」「保持時間が」とHSPが既知の溶媒との相互作用が実数で得られている必要がある。
これまでは、そうしたXを研究者がまるッと決めて0,1の符号にしていた物を、実数そのものを使う。
例題：パルスNMRの緩和時間の解析
例えば、表面をシリカでコーティングした酸化亜鉛粉末表面に対する、溶媒の拘束性がパルスNMRの緩和時間の測定によって解析されている。
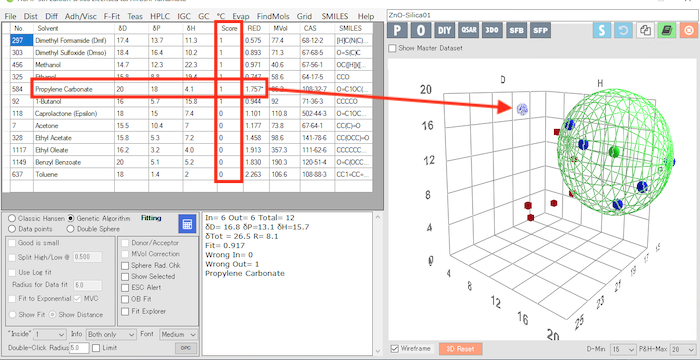
溶解球の中心は[16.8, 13.1, 15.7]になり、塗りつぶしの小さな緑の球が表示されている。
（中心の位置や半径は計算のたびに少し変わる。このぐらいのデータ数では、どちらが正しいとは言えない）
この結果は定性的な結果で、大きな緑の球を堺にして、道の溶媒が球の内側に来れば、自分が定義した良と同じくらい良であると理解できる。
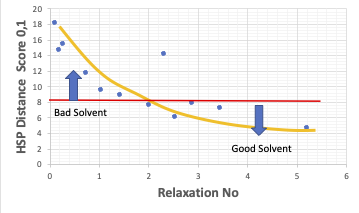
それでは、この場合は”良”か”貧”はRelaxation Noで与えられている。
DMF CAS:68-12-2 [H]C(N(C)C)=O がRelaxation No=5.2で定量的には一番よくとかしている。
それではDMFのHSPを定量的なHSPのSphereの中心にしてしまって良いかというと、そこまで簡単ではない。そのようなことをしてしまうと、DMF以外にもっとよく溶かす溶媒はないという事になる。
そこで、定性的に求めた玉ねぎの内部から、HSP距離とRelaxation Noなどの定量値が最も高い相関になる中心を探索する。
その方法は遺伝的アルゴリズム法(GA法)を使う。
通常の山登り法で傾きの大きい方へ探索をするとLocal maxから抜け出せないことがある。
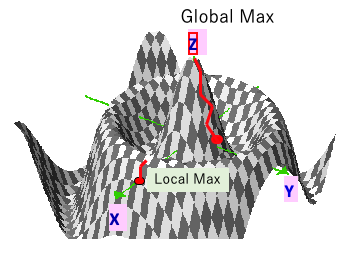
そこで、多次元空間に複数のSphereの中心値をばら撒く。
そのSphereの中心値と各溶媒への距離を計算する。
そしてその各溶媒への距離とRelaxation Noで一番相関が高くなるSphereの中心値を勝ちとする。
そして、適者生存の法則でより適者を求めていく。その際に交叉と突然変異も導入する。
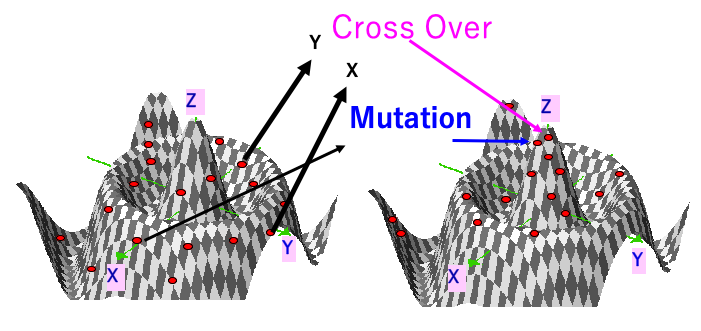
そうした探索を数世代続けると、一番高い山を見つける可能性が高い。
（グローバル・マックスを見つけるのはとても時間がかかるが、有限の時間内でそれなりの答えを探索してくれる。）
実際にやってみよう。
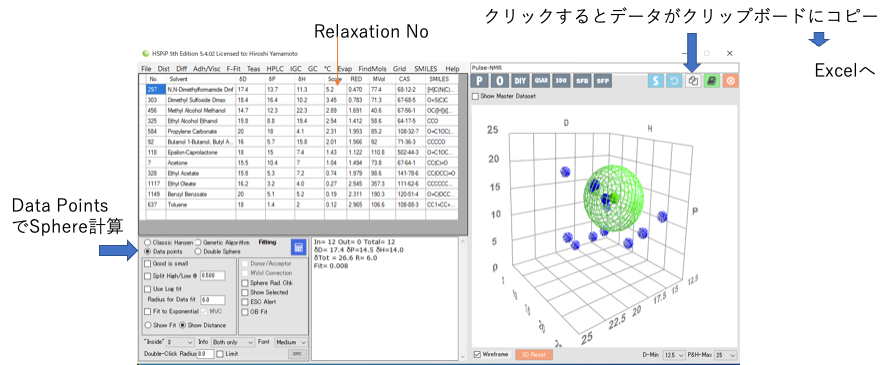
Sphereの計算が終わったら、テーブルの中身をクリップボードにコピーしてエクセルにペーストしてグラフを書く。
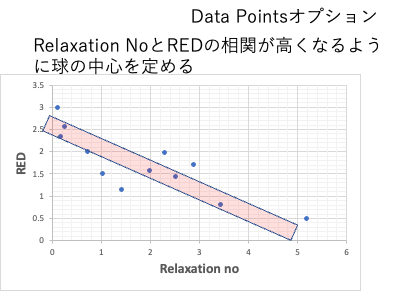
この様な形で、Relaxation NoとREDの相関が取れると、最もよく溶解する溶媒は球の中心になる。
つまり、定性的な球の中心[16.8, 13.1, 15.7]から[17.4, 14.5, 14.0]へ中心の位置がずれたことになる。
あくまでも、相関係数が一番高くなる球の中心を求めてしまうので、１点が大きく外れる異常値の場合、探索結果が信用おけなくなる。その場合にはマニュアルでその溶媒を取り除く（Scoreに”-”を入れる）などの処置をする必要がある。
パルスNMRのように、初めから実数の結果が得られているなら使わない手はない機能だ。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。