次世代HSP技術

2024.7.14

解析例トップ >

GUIのいらないMI用ツールの解説

HSPiPにはCLIライセンスというのがある。Command Line Interfaceの略で、GUIを使わずにSphereやY-MBの計算を行うことができる。
Y-MBはHSPの値も吐き出すが、MIを行う上で重要なパラメータも多く作成する。
そうした機能を、CLI -Proとして別モジュールで販売することも考えたが、Abbott先生は気に入らなかったようだ。HSPiPはバージョンアップは（今のところ）無料なので、新しい機能をつけ加えても、売り上げには貢献しない。（必要なところには行き渡った？）そこでGUIのいらないMIツールに関しては、HSPiPとは別に、YMB24Pro4MIツール群の形でリリースした。HSPiP一般ユーザー向けのツールではない。HSPiPのコーポレート、CLIライセンスの大口ユーザーは、問い合わせていただきたい。

液相拡散係数　2024.8.9

ある溶質が液体中をどのぐらいの速度で拡散するか？のデータが化学便覧に記載されている。

これを新しい距離の式で解析してみた。
しかし、そもそも、拡散係数の高い化合物は、溶媒と良く相互作用しているのだろうか？　それとも弱く相互作用しているのだろうか？
ちなみに、水溶媒で一番拡散係数が高い溶質は水である。しかしベンゼン溶媒で一番拡散係数が小さいのはベンゼンである。
現在の距離の式は、よく溶解するものの距離が短くなるように係数を探索する。
従ってScoreのデータの取り方はよく考えなくてはならない。

バイオ系酸化防止剤　2024.8.6

ビタミンCやお茶の抗酸化剤カテキン類は、カルボキシル基やフェノール性の水酸基を持つので新しい距離の式が有効だろうと考えて解析を行ったが、予想を覆す結果になった。

透過現象 2024.8.2

ある化合物が防護用の手袋を透過する時間、破過時間(Break Through Time)や、さらに皮膚を透過するKp(cm/hr)はHSPとどういう関係にあったのだろうか？
こちらにまとめてある。正直にいうとHSPはあまり関与しないという結果だった。

今回はさらに新しい距離の式で評価を行った。多くの洞察を与える結果となった。

YMB24Pro4MI-Tools　2024.8.2

飲み会の前に、ちょっと試しにスタンドアローンタイプのアプリケーションを作成してみた。簡単にMac, Windows, Linuxで動作するアプリができた。

元々、GUIなど使わずに、コマンドプロンプトから使う設計なので、アプリケーションといっても味も素気もない。ネットワークにアクセスする必要がない。ハードディスクの読み書きは行わない（コピペのみ）利用期限が設定できる。もう少し動作チェックしたのち、MIユーザーへ配布する。その後Webアプリの提供は終了する。
ライセンスの使用者数を限定するのは、私には荷が重い。どうしても利用者数無制限の（高額な）コーポレート・ライセンスになってしまう。それでも年契約できるからまだいいか。

酸性顔料、塩基性顔料の分散 2024.7.30

デンマーク(Hansen先生の母国）で画家は筆を洗うのにシンナーを使っていた。そしてシンナーは健康には良くない。（日本でも印刷工が胆管がんになるなど、今でも問題が出ている）そのシンナーをハンセンの溶解度パラメータ（HSP)を使って他の安全な溶媒に置き換える。それがHSPの始まりだ。
そこで顔料、ポリマー、溶媒の組み合わせの研究は非常に多い。

HSPiPの中にもオランダのワーヘニンゲン大学のScheutjensとFleerが開発した、SFBoxが搭載されている。しかし、私は中身をあまり理解していないので使い方を提案できていない。
ここでは、SFBoxの利用の話ではなく、HSPが長年答えることができなかった、酸性顔料、塩基洗顔料の分散の話だ。溶解度パラメータはHildebrandの”The solubility of nonelectrolytes”が大元なので、酸性、塩基性を扱えない。そこで塗料業界では、とても限定的な利用しかされてこなかった。しかし、無機物の分散にはLewisのDonor/Acceptorが重要だとわかってきたので、顔料へも適用してみた。

Y-PBの最新版？　2024.7.28

Y-MBは低分子用の物性推算機能だ。HSPiPユーザーであればよく使う機能だろう。これについてはver.6で（新しい機能は搭載されなかったが）全面的に書き換えた。中分子や官能基を多数持つ分子のOvershootingは圧倒的に減って解の安定性は高くなった。
同様にpolymerSmiles(繰り返しユニットをXで挟むSMILES)からポリマー物性を推算するY-PB(ver. 5.2に搭載)は2022年に計算アルゴリズムを全面的に変更していた。

Y-PBはDIYのPolymerタブから使える。

ところが、ver.6のリリースの時に変更するのを、私が忘れたようだ。
Pro版のY-PBを作っていて、計算結果がHSPiPのver.6のものと違うので発覚した。
というか、正確にいうと、新しい計算式を作って、タイトルをYPB22に変えただけで、読み込み関数を何もいじっていなかった。まー、コロナの激しい時で、まともじゃなかったって言い訳しておこう。

解熱鎮痛剤 2024.7.29

***

Loopボタンを押して構造を確認してみると、カルボキシル基と他の官能基を持つものが多い。Paracetamol（アセトアミノフェン）は以下で説明したが、こうした解熱剤の溶解性に関しても新しい距離の式が有効だ。

複数の官能基を持つ場合の混合則 2024.7.28

自慢ではないが未だにわからない。HSP50周年(2017年)の時からわからないと言い続けている。逆ギレして仕舞えば、HSPの混合則だって体積分率平均が正しいとは言えない。例えば、Paracetamolの場合、どう取るのが正しいのだろうか？

アセトアミノフェンの定量的溶解性にも記載しているが、難しい。そこで全部計算して一番よく合うものがどれかをみる。カッコよく言えばデータ駆動型研究とも言えなくない。HSPだけで説明できない時に考えるネタを与えてくれる。

液液抽出をHSPで考えるのは難しかった 2024.7.21

2010年当時は、水とオクタノール、ジエチルエーテル、クロロホルム、四塩化炭素、ベンゼン、ヘキサンの液液平衡をHSPで考えるのは難しかった。ある化合物の水とのHSP距離、有機溶媒とのHSP距離で簡単に計算できると思ったのだが。

例えば、オクタノールのKdの値はHSP距離で考えるより、単にHSPで使っている分子体積で考える方がよっぽど良かった。今回はdHの値をいろいろと分割し、距離の式を試すことができるようになったので、再評価を行った。

HSP2Go 2024.7.19

溶媒のHSPとSphereのHSPを貼り付けると拡張現実、ARとして表示することができる。
2016年にポケモンGoが流行ったときに作ったソフトだが、Processingの最新版をインストールしたらそのまま動いた。まー現実の方は入れなくても簡単に3次元表示のプログラムは作れるので有用だ。いろいろインスパイアーされるのは楽しいことだ。

Flory-Huggins のχパラメータ 2024.7.18

格子モデルに基づく高分子溶液の統計熱力学理論
数珠状につながった玉（高分子）とつながっていない玉（溶媒分子）を考えることにより、混合エントロピーを導く。

ポリマーのHSPと溶媒のHSPがあれば、2.13式からχパラメータが計算できる。
今回、酸・塩基、ドナー・アクセプターと距離の式を拡張した。χパラメータと距離の式を見ていこう。

QSphere：量的な問題を解く 2024.7.17

HSPiPのScoreは基本的には0,1である。

dDを分割したり、dHを５タイプに分割した新しい距離の式を作成した。さらにプログラムを拡張して、Scoreに実数を使うQSphereを作成した。これは、距離と実数が一番高い相関になるように玉ねぎの中心を求める。より多く溶解、より長く分散などを考える時にはQSphereは有効だ。無機物の分散では、yED/yEAが重要になったりする。

HSPと表面張力 2024.7.15

表面張力の推算に関してはpirikaのHPで詳しく解説している
表面張力の推算法
表面張力の理解のために
このところ、液体の接触角をHSPで取り扱うケースが増えてきた。水素結合項δHの取り扱いを理解していない解析があるので、HSPと表面張力の違いを解説しておく。
Abbott先生は表面張力は嫌いなので、HSPiPには搭載されない。

3次元では足りない？ 2024.7.14

旧来のHSPであれば[dD, dP, dH]と3次元なのでハンセン空間、ハンセン球から溶解性や分散性を判断できた。MIで用いる分にはグラフィックは考えないで良い。しかし、MIユーザーとしては、次元削減方法は習得しておく必要がある。
主成分分析(PCA)を用いた次元縮退

新しいHSP距離 2024.07.11

2017年、HSP50年記念講演会で、分散項dDのdDvdw, dDfgへの分割を発表した。
さらに、dH項の分割を試みた。しかし、HSP距離の式が作れなく、実際の利用にまで至っていない。量子ドットの分散を例に新しいHSP距離の使い方を解説する。
アバタ・チュートリアル
No12. 量子ドットのようなナノ粒子のハンセン溶解度パラメータを得る方法
PirikaNews2024年7月号
も合わせて読んでほしい。

新しい溶媒混合則

2024年1月にリリースされたY-MB24のHSP値推算ルーチンでは、混合溶媒は体積平均で計算するのでは無い。しかし、HSPiPではそのような取り扱いができない（とても面倒）ので昔ながらの計算方法をとっている。これはMIユーザー用の機能として公開していく。

ブログ：次世代ハンセン溶解度パラメータ(HSP²)　混合溶媒の混合則　2024年3月20日

ハンセン空間中の分布を3次元で見る　2024.7.28

研究者の定義した”良い”溶媒がハンセン空間に集まって来るわけではない事は以下で説明した。HSPiPは持っているのが前提なので、溶媒のHSPの値を3次元で見るのも簡単だ。ここでは、Plotlyという3次元表示用のWebアプリを簡単に利用する方法を解説する。HSPiPを持っていない方に渡す、Webページに載せるなど利用方法も多いだろう。

タブ区切りのデータがあれば、自動的に表示用htmlファイルを作るWebアプリを作った。視覚的にはハンセン空間はdD軸は長さが倍になっているので（距離の式でdD項の前に4が付くので）HSPiPの表示とは少し異なる。主成分分析を行なった上で３次元にプロとおするのは良い。

ハンセンの溶解球の誤解：良いものが集まって球を作る。2024.7.13

研究者が定義した良いものが集まるわけではない。HSPが近いものが、同じような性質を持ちHansen空間中で集まるだけだ。研究者にとって良くない、長い緩和時間の溶媒が集まってしまうことだってある。

良いとか悪いというのは、あくまでも研究者の主観であることをお忘れなく。

その溶解はHSP依存だろうか？

HSPiPを開発している私が言うのもなんだが。その溶解、分散はハンセンの溶解度パラメータでしか説明できないものだろうか？

特に第３周期以降の原子が絡んでくると、d,f 軌道の空軌道が電子を受けとったり解釈が難しくなる。HSPだけでなく、他の識別子で重要なものを選択し、総合的に判断していくことがMIstには重要になる。MIツールの中の識別子ジェネレータと変数選択重回帰法の解説をしよう

無機物の分散に酸性、塩基性は影響するだろうか？

2017年のHSP50周年記念講演会でY-MBでElectron Donor/Acceptorを推算する方法を発表した。HSPiPではプロトンのDonor/Acceptorなので、活性水素を持った化合物以外には関係ない。
化学総説 No.18 1978年 「情報化学」　日本化学会編の125ページには、酸化物の酸性、塩基性が分類されている。こうした酸化物はLewisの酸/塩基で考えなくてはならない。そうした相互作用を合理的に取り込める距離の式が作れなかった。しかし、MI的に使うのであれば良いので、HSPiPとは離れMIユーザーに提供していく。
ここでは、水素結合項の分割について解説する。

SOMを使ったMy周期律表

MI用ツール群の紹介

HSPiPのGUIを離れ、YMBの推算値をMI用のインプットに用いる使い方が増えている。Excelのoffice scriptやJSpreadSheetなどを使って簡単にMI用のDescriptorを作るWebアプリを作成している。さらに機械学習に使う便利なツール群の整備も進んだ。これはMIユーザー用のツールだ。
ブログ：ハンセン溶解度パラメータ(HSP)推算がExcel上で動くようになった。2023年4月29日
ブログ：Power AutomateでY-MB計算の自動化　2023年5月4日

2024.7.12　MIユーザーには次のMIツール群(Webアプリ)を提供している

Sphereの拡張

定量性ある「Sphereの中心」の意味について新たに解説を加えました。2023.4.24

CLIライセンスの利用：

関連ブログ：生物等価性とHSPiPのCLIライセンス

主成分分析(PCA)を用いた次元縮退

HSPをドナー、アクセプターなどに分割していくと、3次元までしか表現できないSphere法では視認性が悪くなる。そこで主成分分析(Principle Component Analysis)を用いて次元縮退することを考えた。
関連ブログ：3次元HSPから7次元HSP²へ。DXを使ってHSP²をAXしよう。

もし、HSPiPを使っていて、うまく解析できないなどの不具合があった時には、これらのことを考えてみると良いかもしれません。

構成は、予稿の1-3はHSP50会議の前に読んでくることを想定しています。
そこで展開される新しいアーキテクチャを使って実際に問題を解くことをキーノート・スピーチの1-2で行っています。

HSP²

ハンセン溶解度パラメータ(HSP)50周年記念の講演会が2017年に行われました。

そこで、山本は,
Hansen-Hiroshi-Steven Solubility Parameters for Prediction(HHSSPPでHSP² )を発表しました。
これは後50年*50年、HSP² が使われるようにとの拡張を含んでいます。

残念ながら、ここで発表した機能全てがHSPiPに搭載された訳ではありません(と言うか、まだほとんど(2022年現在)搭載されていません)。また、HSPiP本体に載せるのではなく、GUIなしで使う、CLIライセンス用プログラムへの搭載を考えています。（プロ用の機能）

ユーザーからのフィードバックがなければ、先生たちがHSP² 用の機能をHSPiPに搭載する事はありません。（コンサル契約している所には、必要に応じて別プログラムで提供することにしています。）

Dr Yamamotoによる次世代HSP² 、 Hansen-Hiroshi-Steven Solubility Parameters for Prediction(HHSSPP=HSP² )

予稿

Preprint-Part 1

関連ブログ：距離を極めれば、何でも溶かせる？

Dividing the dispersion term (δD) and new HSP distance 日本語版
HSPの分散項を示すδDは実は、”推算”といった意味では非常に難解でした。これまで、HSPに限らず様々な溶解度パラメータは原子団寄与法で推算する事が多かったのです。
その際に、原子団が0個（何も無い）ならδDもゼロになるはずです。ところが、定数項を０にして、原子団の寄与を求めると計算が破綻してしまうのです。

例えば、普通の直鎖炭化水素は、δP=δH＝0となり、δDの値しか持ちません。ハンセン先生はそこを基底状態としてHSPの根幹を作り上げて行きました。基底状態というのは分子間力が相対的に最小になると言った感じでしょうか。

しかし、パーフルオロの炭化水素、エーテル化合物が出てくると話が困ってきます。フッ素化合物は分子間力が小さく、蒸発潜熱が低く、分子体積は大きめになります。そこで、δP=δH＝0で、δDが炭化水素と比べとても小さくなります。

また、シリコーン化合物も分子間力が小さく、蒸発潜熱が低く、分子体積はかなり大きめになり、δDはパーフルオロの炭化水素、エーテル化合物に近くなります。でも両者は混じりません。

そして希ガスのSP値を検討していて１つ気づいた事があります。希ガスとパーフルオロの炭化水素、エーテル化合物の分子量、沸点曲線はほぼ同一になるという事です。

希ガスは非常に弱いVDWの分子間力しか持ちません。つまり希ガスとパーフルオロの炭化水素、エーテル化合物は分子の大きさだけに基づいた分子間力を持ちます。それを、δD_VDW と定義します。これは希ガスとパーフルオロの炭化水素、エーテル化合物で検量線を引いて、分子体積から一律に求まる値です。
そして、δDの残りのエネルギーを、原子の種類や原子団によるエネルギーとしてδD_fgと定義します。
δD² = δD_VDW² + δD_fg²
の関係が成立します。

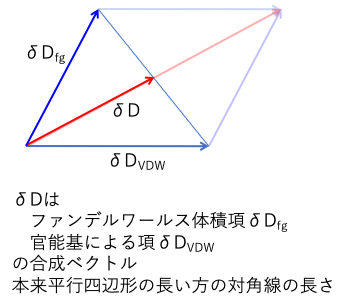
それを本来の長さの半分に定義してしまったので、距離の式でδDの差分の前には4.０という係数が必要になった。

このようにδDを分割する事のメリットは、HSP距離の計算式のδDの前に入る4.0と言うファクターがいらなくなる事です。

Distance₁₉₆₇ ={4.0*(δD1-δD2)² +(δP1-δP2)² +(δH1-δH2)² }^0.5

この４.0の説明は色々ありますが釈然としないものばかりです。

Distance₂₀₁₇ = {(δD_vdw1-δD_vdw2)² +(δD_fg1-δD_fg2)² +(δP1- δP2)² +(δH1-δH2)² }^0.5

つまり、
4.0*(δD1-δD2)² =(δD_vdw1-δD_vdw2)² +(δD_fg1-δD_fg2)²
が、おおよそ、成立していると言う事です。

メリットはデメリットで、HSPが４次元ベクトルになってしまい、グラフで表示するのが難しくなりました。ただ、分子の大きさだけに基づく、δD_vdwを無視して、δD_fgとδP、δHだけで評価しても結果は大きくは変わりません。

特に、Materials Informaticsなどで結果を使う分には、次元の高さは問題ないので、CLIライセンスバージョンに組み込む事が考えられています。

例えば、次のケイ素化合物とフッ素エーテルは、以前のHSPで見ると非常に似通っています。
Distance₁₉₆₇ = 2.0
ですので容易にお互いが混じると考えてしまいます。

しかし、
Distance₂₀₁₇ = 8.5
と大きく異なります。

これらの系で実際に試した事はありませんが、フッ素オイルとシリコーンオイルは溶け合わないのは不思議なこととして知られています。そうした問題を解決するには、このHSP² 技術は有効でしょう。

	Smiles	dD	dDvdw	dDfg	dP	dH
Dimethoxydimethylsilane	CO[Si](C)(C)OC	12.82	9.88	8.16	3.19	4.03
1,1,2,2,2-Pentafluoroethyl 2,2,3,3,3-pentafluoropropyl ether	FC(C(COC(C(F)(F)F)(F)F)(F)F)(F)F	12	12	0.02	3.59	2.88

Preprint-Part2

δNet parameter which hid for 50 years 日本語版
元々、HildebrandのSP値は正則溶液に対するものでした。正則溶液の定義としては、溶質と溶媒の間の凝集力がロンドンの分散力のみの場合をいいます。それでは何かを溶かす前の溶媒自体の”正則性”を考えてみます。

RT（ガス定数*温度）を無視すれば、SP値は次のように書く事ができます。
SP = sqrt( Hv/Volume)
つまり、分子体積(Volume)が倍になっても、蒸発潜熱(Hv)が倍になるのであれば、SP値は同じになります。
多くの場合、溶媒の系列が同じであれば、傾きや切片によって多少変化しますが、この関係はおおよそ満足します。

分子体積と沸点の間には、次図のように、溶媒の系列が同じであれば、ほぼ同一の曲線上に乗る事が知られています。 分子体積のルートを取るとこれは直線になります。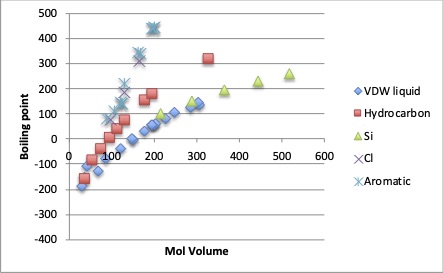

また、沸点と蒸発船熱の間には、Troutonの通則と言うのがあり、沸点での蒸発潜熱を沸点で割った値は、85 J/(mol·K)となる事が知られています。例外となるのは水素結合性の水、低分子量のアルコール、カルボン酸化合物です。同族体であれば分子の大きさが決まれば沸点が決まり、沸点が決まれば比例して蒸発潜熱が決まることになります。

そこで、Troutonの通則、沸点での蒸発潜熱を沸点で割った値が、85 J/(mol·K)となる溶媒を正則溶媒と呼ぶこともあります。つまり、エステル化合物であろうが、エーテル化合物であろうが、沸点が同じなら、蒸発潜熱は同じになります。

水素結合性のアルコールは、水素結合のネットワークを作ります。
そこで、沸点ではそのネットワークを切るのに余分なエネルギーが必要になります。

HSP² では、Troutonの通則を25℃へ拡張し、正則溶媒部分をδ_regとし、残りをδ_Netと定義します。計算に必要な、δ_totと分子体積、沸点は既知ですので、簡単に値が求まります。

基本的に、
δ_Netの大きな溶媒は、δ_Netの小さな溶媒とは混合しない。
δ_Netを大きくする官能基を持ったポリマーは、ガスバリアー性が高い。
など正則性からのズレだけが関与する物性も多い事が明らかになってきています。

Preprint-Part3

Donor/Acceptor interaction 日本語版
実は、HSPは既に水素結合項をドナー/アクセプターに分割しています。まず言葉の定義ですが、HSPiPに搭載されているのは酸/塩基でドナー/アクセプターではありません。
Abrahamの酸塩基を推算し、それを水素結合項に割り振っています。
また、取り扱い上も

Rule 1: δH² = δH_acid² + δH_base²
Rule 2: δH_acid:δH_base = Abraham Acid:Base
Rule3: AbrahamAcidが0の場合δH_acid=0、δH_base=δH

水素結合項にドナー/アクセプター性を割り振ってしまいます。
すると、例えば、δHが非常に小さな化合物、例えば、四塩化炭素(δH=0.6)のδH_Acid、δH_Baseはとても小さくなり、溶解性にほとんど寄与しなくなってしまいます。

Gutmann ドナー数(DN), アクセプター数(AN)を推算する式を構築し、その値をAbrahamの時と同じ方法で、δH_Donor、δH_Acceptorに分割したり、Beerbowerの方法に従って分割したりしましたが、HSPの距離の式までは構築できていません。

HSP² では、現在のところ、δH_Donor、δH_Acceptor、DN, ANを含めMaterials Informatics用の識別子として用いるのが現実的な利用法になっています。

キーノート・スピーチ

以上の、HSP² の３つの拡張に関する予稿を読んだと言う前提で、次の２つのキーノート・スピーチを行いました。

Yamamoto Keynote Speech1

(英語版）
今までのHSPの決定方法と、その問題点、改良方法を概説しました。特に、これまではδDに関しては大きく問題にされる事はありませんでした。しかし、δDには分子の大きさだけで決まる部分と、原子種（原子団）による効果が合わさったものである事がわかりました。δP、δHに関しても、様々な方法を組み合わせることによって、データベース中のオフィシャル値の検証も行いました。また、温度の影響を新しく見積もる方法を開発しました。

Yamamoto Keynote Speech2

（英語版）
正則溶液理論から導き出される結論として、分子の溶解度パラメータを正則溶媒としてのδ_regと、正則溶媒から外れるδ_Netに分割する方法を開発しました。また、Lewis Electron Donor(ED)と Electron Acceptor(EA)を予測する式を構築しました。そうした様々な分割手段を組み合わせると、クラッシックなHSPでは、ほぼ同じHSP値になるエステル、アミン、カルボン酸が全く違う見え方になってくる事がわかりました。

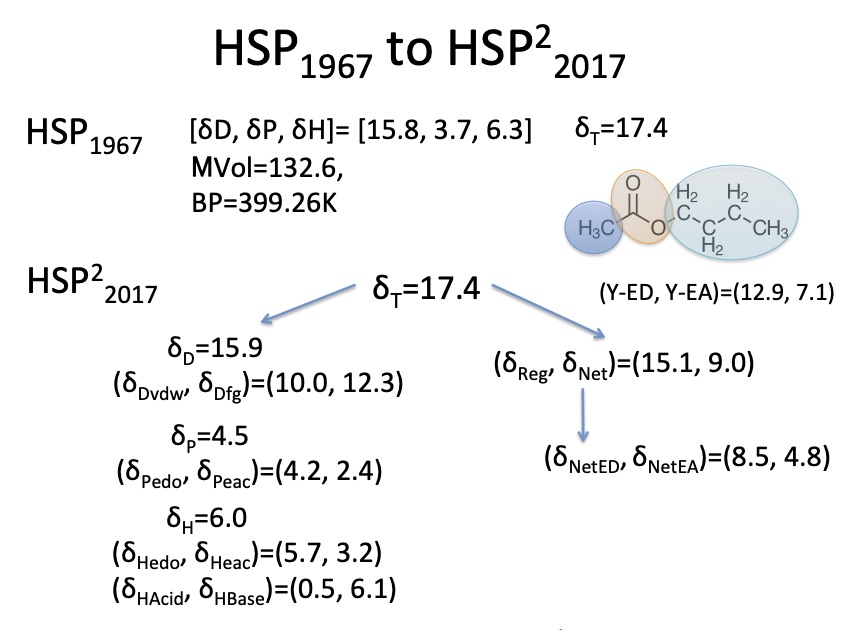
キーノートスピーチの1,2に関しては、HSP勉強会(2017年９月）で日本語で発表しています。

---

Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。