Chapter 17, It’s your call (Rational Selection of Chemical Protective Gloves) 

If you had to recommend the best gloves to use in situations that could be literally life or death, what would you do? To be more specific, what gloves would you recommend to hospital staff so they can safely handle immensely potent cytotoxic drugs of the type used in chemotherapy?

One approach you could adopt is to insist on glove permeability tests for all cytotoxic drugs on all relevant gloves. But this just isn’t practical.

An alternative approach is to use chemical intuition: “It seems to me that glove X should have no problem with cytotoxic chemical Y because they are chemically incompatible.” But would you then have the courage to handle these chemicals all day with the gloves that you have intuited should be OK? We wouldn’t.

In the absence of specific testing, the approach we favour is a rational, numeric approach. The numbers it produces cannot be accurate, but represent respectable estimates of what can be expected. But we don’t need high accuracy itself. What we need is a large margin of safety. If we estimate that a potent drug would have a breakthrough time of 60 minutes, it doesn’t really matter if the real value is 30 minutes or 120 minutes; in neither case would we volunteer to wear those gloves for a whole morning. But if we estimate that the breakthrough time is 360 minutes, we don’t mind if it’s really  300 or  600 minutes, the margin of safety (given that these gloves are worn for significantly shorter periods whilst handling the drugs) is relatively large enough for us to wear the gloves with confidence.

Happily, we have an excellent methodology to make this numeric estimate. We know from the Diffusion chapter that Permeability=Surface Concentration x Diffusion Coefficient. And we already know that a large HSP mismatch between chemical and polymer reduces the surface concentration and therefore reduces the permeability. A measure of the HSP mismatch is the RED number, so a large RED means low permeability and therefore long breakthrough time.

We also know some things about the diffusion coefficient. First, because we are handling very potent chemicals, they will tend to be in low concentrations, so the relevant diffusion coefficient is likely to be the D₀ value, the “intrinsic” low-concentration diffusion coefficient. There will never be enough of the chemical to give the orders of magnitude increase in diffusion coefficient that could give dramatic decreases in breakthrough time, nor significant swelling of the gloves. Second, we know that the molecular shape and size makes a big difference. There are no general rules for the effect of molar volume but for the materials used for gloves the approximation from the previous chapter that doubling the molar volume halves the diffusion rate would be a conservative choice. We know, too, that linear molecules generally wiggle their way through with more ease than branched, cyclic and/or aromatic molecules. Once again, we can make a conservative estimate of a halving of diffusion rate for a given molar volume if the molecule is not especially linear. For many of the complex cytotoxic molecules we can be confident that this is much too conservative.

We almost have all the tools we need to estimate breakthrough times for cytotoxic molecules through typical gloves. But we are missing a key bit of data. Although a “large” RED undoubtedly means a “longer” breakthrough time, how do we actually estimate the breakthrough time for a given RED number? Fortunately there are HSP correlations for the most common types of gloves that can be used for this purpose.

Let’s take a specific example. From the Attacking DNA chapter we know that Cyclophosphamide has HSP [17.5, 11.9, 12.6] and molar volume 279.

Now let’s look at a table of glove properties. Along with the glove type and breakthrough times is given the upper and lower molar volumes of molecules used in the correlation. This is a useful guide for comparing to the molar volumes of the chemical under consideration. “All” mean that there were no limitations on the solvents.

Glove Type - Breakthrough	δD	δP	δH	R
NR 20 MIN (58 to 178)	17.50	7.30	6.50	5.10
NR 1 HR (61 to 178)	16.60	9.10	4.40	10.00
NR 4 HR (58 to 178)	19.00	12.60	3.80	13.30
BR 20 MIN (71 to 110)	16.50	1.00	5.10	5.00
BR 1 HR (71 to 126)	15.80	-2.10	4.00	8.20
BR 4 HR (All from 71)	17.60	2.10	2.10	7.00
NAT 20 MIN (61 to 267)	14.50	7.30	4.50	11.00
NAT 1 HR (56 to 325)	15.60	3.40	9.10	14.00
NAT 4 HR (up to 325)	19.40	13.20	7.70	19.00
PVC 20 MIN (61 to 267)	16.10	7.10	5.90	9.30
PVC 1 HR (61 to 267)	14.90	11.10	3.80	13.20
PVC 4 HR (up to 149)	24.40	4.90	9.90	22.70
PVA 20 MIN (All)	11.20	12.40	13.00	12.10
PVA 1 HR (All)	15.30	13.20	13.50	8.80
PVA 4 HR (All)	17.20	13.60	15.40	10.90
PE 20 MIN (All from 40)	16.90	3.30	4.10	8.10
PE 1 HR (All from 40)	17.10	3.10	5.20	8.20
PE 4 HR (All from 56)	24.10	14.90	0.30	24.30
VIT 20 MIN (All)	10.90	14.50	3.10	14.10
VIT 1 HR (56 to 178)	16.50	8.10	8.30	6.60
VIT 4 HR (All to 178)	13.60	15.40	8.60	14.40
NEO 20 MIN (75 to 178)	17.60	2.50	5.90	6.20
NEO 1 HR (69 to 178)	19.00	8.00	0.00	13.20
NEO 4 HR (61 to 266)	14.60	13.90	2.30	15.90

 

If the Cyclophosphamide is compared to the 20min Nitrile rubber gloves [17.5, 7.30, 6.50] and radius 5.1, the RED number is 1.5. If the comparison is for solvent breakthrough times of 1 hour then the glove HSP values are different [16.60, 9.10, 4.40], radius 10.0 and the RED is much reduced, to 0.88 The radius is larger because the increased time allows less favourable molecules to diffuse through. By extrapolation/interpolation it’s possible to say that for a RED of 1 the breakthrough time would be 45 minutes. In other words, we have defined a radius of Nitrile which places Cyclophosphamide in the danger category of “soluble” and therefore we can assume, all things being equal, that it will diffuse through in 45min if present in the sorts of concentrations typical of the permeation cell breakthrough experiment.

But what are those concentrations?

Again, we can make rational estimates, but quickly add that these can be improved upon with experimental swelling data for a given glove type.

Breakthrough time     Extension of breakthrough time        Estimated       Estimated

    in Permeation cell               for very low concentrations                  uptake, %                D_max/D₀

                <20 m                                                      4.0                                                   25                50     

                20-40 m                                   1.9                                                   15                10

                40-60 m                                   1.5                                                   10                  5

                60-240 m                                 1.1                                                     5                2

                >240 m                                    1.0                                                   <3                  1

 

For very quick permeators, the glove material could easily hold 25% of the permeant. For very slow permeators the glove will probably hold <3%. We can then use the typical curves of diffusion coefficient v concentration to estimate the Dmax/D₀ at those concentrations and, therefore the extension of breakthrough time for very low concentrations.

The above argument is sound, but the actual numbers cannot possibly be accurate. But we don’t need extremely high accuracy. If we estimate that our intrinsic breakthrough time is 45min and if we think (from the above table) that we therefore have a factor of 1.5 which takes us to 70min this really doesn’t alter our judgement very much. Whether it’s 45min or 70min we’re not going to use those gloves for a whole morning.

And when the gloves give us >240min we don’t care if the extra safety factor is 1.1 or 1.2, we’re already in quite a good safety zone.

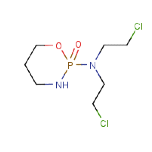
If we continued with the Cyclophosphamide example we would add our final factor, the “shape/size” factor.

 

This is clearly not a linear molecule – it’s both branched and cyclic, but then so are some of the molecules used in the breakthrough experiments. So there’s no room to give a significant change of D₀ on those grounds. Its molar volume is about 50% larger than any used in the breakthrough experiments so maybe we can add a factor of 1.5 to the breakthrough time. We can finally arrive at an estimate of 45 x 1.5 x 1.5 = 100min.

And because it’s good practice to wear two sets of gloves (in case one gets accidentally holed), and because breakthrough time goes as thickness squared, two gloves take the breakthrough time to beyond 200 minutes.

For Natural Rubber (latex) gloves the basic estimate is <20min. Even allowing for some adjustments upwards, it seems clearly inappropriate to think of using latex gloves, even two pairs.

For Butyl gloves, the starting estimate is >240min because Cyclophosphamide’s RED number at 20min is 2.8 and at 4 hours it’s 2.0. There is no extra 1.5 for solubility because a 240min diffuser is already at low concentrations. So we can add a 1.5 for shape/size giving use >360min or >6 hours. That’s not bad.

Polyethylene has such a large HSP distance from these sorts of drugs that such gloves are obviously excellent barriers from a diffusion point of view. However, they are easily ripped and can’t be recommended for such critical use.

As this may be a matter of life and death, let’s repeat ourselves. The calculations on the Cyclophosphamide and Nitrile gloves cannot possibly be highly accurate, but they are good enough to say that Nitrile gloves are not recommended for long-term use. But for short-term use, with a rule that two pairs of gloves should always be worn (and extra rules if there is any chemical incident), they look OK. Similarly, the calculations with the Butyl gloves cannot possibly be accurate, but they are more than good enough to say that there is a considerable margin for safety for a whole morning or for cleaning up significant spills. And that’s all we need.

Of course it’s not up to the HSP scientist to make the final recommendations. A large number of other considerations have to be taken into account. For example, whilst Butyl gloves are excellent barriers, they aren’t good for delicate handling of medicines. Latex gloves are very comfortable, but the barrier properties for these sorts of chemicals are much too poor. Nitrile gloves are very comfortable and are a better barrier than latex. So a hospital committee might decide, for example, that Nitrile gloves are a good compromise choice provided that (a) two pairs are worn, (b) the outer glove is replaced after 30min and (c) if there is any serious incident (e.g. a spill of the chemicals) the user swaps to Butyl gloves.

If you are disappointed by this approach then think about how expert committees reach their opinions on exposure limits of chemicals. They almost never have enough good data to reach a definitive and accurate assessment of the specific risks of a specific chemical. But usually they don’t need that accuracy. Instead they need a defensible set of numbers to say that the risk level is in this range rather than that range. From those numerical judgements all sorts of practical consequences can then flow. They have to make such judgements. If they say that all chemicals are dangerous then we can’t live a practical life. If they say “we don’t have good enough data to form any judgement” then we live a lottery life.

If experts say “no glove is 100% guaranteed to handle all possible cytotoxic chemicals” then their life-saving capabilities for cancer patients will never be practically deliverable by medical professionals. If experts say “we can’t calculate any glove to high accuracies, so just make your own judgement” we are asking the medical professionals to take unnecessary risks, or to wait an excessively long time for experimental results.

So we do the best we can, with the rational tools at our disposal. If you can think of a better method than the one described here, we’d be happy to put a note in future editions of the eBook saying “The HSP estimator method has now been superseded”. Till then, we think it has much to recommend it.

Some like it hot

The above analysis may sound a little academic. Yet whilst we were writing it, Hiroshi hit a painful problem. Unfortunately he hadn’t carried out a proper HSP risk assessment before undertaking a task, and his hand was in pain for 3 days afterwards.

You see, Hiroshi loves cooking with chillies. He decided to make a large amount of chilli sauce and ground up this large supply of chillies.

 

He decided that PE gloves would be a good barrier to the capsaicin in the chillies, but quickly discovered that they were easily damaged, so he swapped to latex gloves. After some time handling the chillies he found that his hands were hurting from capsaicin that had got through the gloves.

We then decided to work out what gloves he should have used. Happily, we’d done the work already. When we loaded the .mol file for capsaicin into the Y-MB estimator (it’s included in the Examples folder if you want to try it yourself), we found the estimate was similar to Cyclophosphamide and the other cytotoxic chemicals.

 

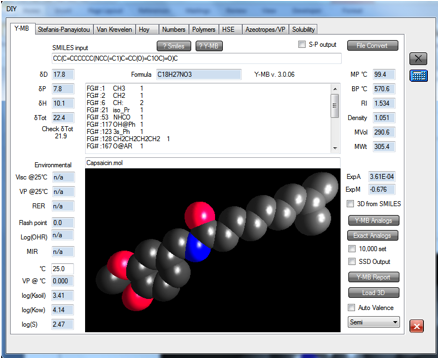
Therefore we can recommend that the next time he has to make chilli oil, he should use two pairs of Nitrile gloves or, if he doesn’t mind the discomfort, PE on the inside and latex or Nitrile on the outside.

Whilst we’re on the subject of chillies, we can address another important question. If you accidentally eat too much hot chilli, what is the best way to remove the pain?

Because the HSP of water is too far from capsaicin, the old favourite, cold beer, is clearly useless. Ethanol is not a great match, but is much closer, so a sip of neat vodka will be helpful. You often hear people say that capsaicin is “soluble in oils”. This is only partly true. Simple oils and fats such as olive oil or lard ~ [16, 1, 5] are too far away in HSP distance to be very effective. Indeed, Hiroshi experimented with extracting capsaicin with olive-oil and found it made a very weak solution. However, they are better than water so that’s one possible reason why milk and yoghurt are so often recommended as a good way to remove the sting of chilli. It seems likely that the proteins in milk are a reasonable HSP match with capsaicin and maybe that’s the real reason that milk/yoghurt are recommended. However, if it’s the fats that are important, remember not to use low-fat milk/yoghurt during your chilli crisis.

 

E-Book contents | HSP User's Forum