Chapter 18, Gloves: from minimum data to maximum insight (Exploring Glove Permeation)

The real world is often full of incomplete data. Like it or not, we have to make decisions with the data we’ve got. This chapter extends the theme from the previous one and shows how HSPiP can take imperfect data and with some good theory, a good modeler and some persistence, create some solid understanding of an important topic – the solvent resistance of gloves.

There are two inter-related criteria for judging the safety of gloves: the breakthrough time and the steady state permeation rate (SSPR). As we will see, ASTM judge the breakthrough time when the permeation rate reaches a certain limit. To understand the importance of HSP for the performance of protective gloves, we’ll remind ourselves of the equation for the SSPR.

SSPR = D_av(C₁ – C₂)/L   [g/cm²/s ]

D_av = D₀D_lm   [cm²/s]

C₁ is the surface concentration (g/cm³ dry polymer), C₂ is assumed to be zero, D₀ is the diffusion coefficient (cm²/s) at essentially zero concentration (or where the diffusion coefficient is indeed a constant), and L is the (dry) film thickness (cm). The log mean average of the diffusion coefficients at C₁ and C_2, is called D_lm.  This accounts for changing diffusion coefficients within the film from D_max at the exposed side to D₀ at side 2 for a typical exponential dependence on concentration: 

D_lm = (D_max/D₀ – 1)/ln(D_max/D₀)   [dimensionless]

HSP immediately affect the SSPR because the surface concentration is higher for a better HSP match. This surface concentration is almost always assumed to be the equilibrium concentration as measured by swelling tests (but see below for acetonitrile in Viton for a case where it is not).

Although we know that HSP don’t affect D directly (for similar molecular shapes, a molecule with a bad HSP match will diffuse at the same speed as one with a good match), D can increase greatly as the concentration increases, so a good HSP match indirectly leads to a high D through this effect.

When D is concentration dependent, calculations are best done with a full-scale modeler such as the one in HSPiP. But if you are keen to do things from formulæ then it is possible to calculate the steady state permeation rate using those given above.

The breakthrough times also have the double dependency on polymer solubility and therefore a double dependency on HSP. Fortunately the HSPiP diffusion modeler can readily handle this complex situation. The main problems are connected with getting the correct data to put into the calculations. There is very little information in the protective clothing literature on diffusion coefficients, much less how they change with the local concentration.

Estimates of the equilibrium swelling concentrtion and D are required to understand what is going on within the glove, and when to be concerned with events on the “safe” side of the protective elastomeric film. When such data are lacking, simple but judicious use of HSP correlations of swelling, breakthrough times, or permeation rates are fully justified, because of the very close connection between the HSP and these phenomena. That’s the logic behind the choice of gloves in “It’s your call”.

Help in estimating D₀ for a given chemical can be found in Figure 1. This figure ranks (from top left to bottom right) the amount of solvent retained in vinyl and acrylic films for very long times (months). This is, in effect, a ranking of their diffusion coefficients at low concentration and essentially the same ranking will be found in films made from different polymers. It is the activation energy required to cause polymer chain segmental motion that determines how readily suitable free volume becomes available for movement of the solvent molecule. These activation energies will be different for different polymers, but the ranking of solvent diffusion coefficients will not change significantly. The larger, cyclic and branched molecules will require more free volume in order to move in any polymer so there is a larger activation energy for these molecules than for smaller and more linear molecules. Figure 1 provides a method to interpolate/extrapolate diffusion coefficients (D₀) on a relative basis in any polymer. The key thing to remember is that although the relative order will remain constant between polymers, the size of the effect will be highly polymer dependent. In a very rigid polymer the difference in diffusion rates between large and small molecules will be much larger than for a highly flexible polymer. The ranking by Shell reported in the Factor 4 section of the Diffusion chapter provided independent confirmation of this fact.

 

Figure 1‑1 Relative solvent retention in vinyl and acrylic films as a function of the size and shape of the solvent molecules. (Source: Hansen, C.M., Doctoral Dissertaton, Technical University of Denmark, 1967, available as a PDF file on www.hansen-solubility.com by clicking on the cover page). Cyclohexyl chloride is retained more than cyclohexanone which is retained more than diacetone alcohol, etc. with methanol being the solvent that gets out fastest.

 

Analysis of permeation data to estimate the diffusion coefficient concentration profile

Diffusion coefficients must be low if a glove is to offer good protection. This implies that either the HSP match must be (very) poor to keep the surface concentration (equilibrium swelling amount) down, or else the challenge chemical has a large molecular size.

Because we don’t have all the required data to hand in order to explain permeation rates and breakthrough times we have to find a rational process for providing adequate fits to whatever data are available. The trick is to find (concentration dependent) diffusion coefficients and (hopefully from independent measurements) surface concentrations that fit both the equilibrium permeation rates and the breakthrough times. Experience shows that the room for adjusting the parameters to attain good simultaneous fits is surprisingly small, giving confidence that the resulting values are meaningful.

When inputting the concentration dependent diffusion coefficients there is no strict requirement to enter values for concentrations above the surface concentration. However it is good practice to make sure that the curve covers the whole range smoothly up to 100% solvent which of course is limited to some value below that for the self-diffusion coefficient since the diffusion coefficients used in the modeler are based on dry film thickness. As shown in the first figure of the diffusion chapter, the diffusion coefficients based on dry film thickness will be somewhat lower than those based on total film thickness. At 100% solvent the diffusion coefficient based on a dry film thickness becomes meaningless. This does not significantly affect the results within the concentration range of usual interest, but should be recognized when solvent concentrations become very high.

We have used permeation data reported in the Chemical Protective Clothing Performance Index, Second Edition, by Krister Forsberg and Lawrence N. Keith (abbreviated F/K). Data from other sources have been used as a supplement to these. The major problem with the F/K data is the lack of information on the surface concentration from equilibrium swelling experiments. A second problem is that the criterion for the breakthrough time is not given. The work reported here started with a breakthrough time defined at having a concentration on side 2 of the glove equal to 0.1% of the equilibrium solubility. This was supplemented by use of the ASTM F739-99a criterion for breakthrough which is a permeation rate of 0.1μg/cm²/min. This is equal to 1.67E-09 g/cm²/s, the units used by the HSPiP modeler.

In the figures below the red line reports the permeation rate at the given time. These values can be read accurately using the mouse over the graph, allowing interpolation to find the ASTM breakthrough time. Values defining the diffusion coefficient profiles were systematically changed until simultaneous agreement was found with both the reported breakthrough time and reported permeation rate. Excellent agreement of this kind could be found in all cases reported below for Nitrile, Butyl, Neoprene, Viton, and Natural Rubber gloves. In one case discussed in detail below (acetonitrile in Viton) it was necessary to include a significant surface condition effect to greatly improve the match with the literature data. A significant surface condition delays the breakthrough while not (necessarily) affecting the steady state permeation rate. It was possible to match permeation data in F/K for natural rubber in some cases, but the data for methanol, as discussed below, are difficult to make consistent.

Our use of specific glove types in the following examples is merely so that the interested reader can identify the specific data from F/K. They, in turn, emphasize that the “same” glove (e.g. “Nitrile”) from different manufacturers can have different properties – though we’ve tried to ensure that our examples are of gloves that are within the normal range expected of each type.

In all the figures that follow, the blue line gives the percentage of the saturated amount in the glove. The red line follows the permeation rate to the equilibrium condition.

 

Toluene permeation in Nitrile glove Ansell Edmont type 37-165

Insight into the mechanism by which the Ansell Edmont Nitrile glove type 37-165 protects against toluene is provided by Figure 2. The F/K data are: Breakthrough time 61 minutes, permeation rate 4000 mg/m²/min, and thickness 0.64 mm. The equilibrium uptake of toluene in this glove type is 0.67 volume fraction (private communication from Dr. Jaime Lara, IRSST, Montreal). Figure 2 was generated using these data by assuming different diffusion coefficient profiles as a function of concentration. The range of possibilities among the variables is surprisingly limited. Emphasis was given to the perfect calculated match of the experimental permeation rate of 6.68E-06 g/cm²/s. Less emphasis was given to a simultaneous match of the breakthrough time because the experimental determination can hardly be expected to exactly match the 0.1% concentration assumption for breakthrough which gave a time of 64.3 minutes. The results found when matching the data using the ASTM breakthrough criterion are discussed below. The agreement is surprisingly good in both cases. A very interesting aspect is the diffusion coefficient profile. A straight line on the log D versus volume fraction plot starting at D₀ equal 1.15E-08 cm²/s and ending at 1.1E-06 cm²/s at the surface concentration was required to match the performance data. The whole permeation process occurs in an elastomeric diffusion region. It can also be seen that further extrapolation of this straight line to the pure liquid gives a diffusion coefficient near 1E-05 cm²/s which is very close to that expected for the pure liquid. This self-consistency is also an important consideration for a correct estimate.

 

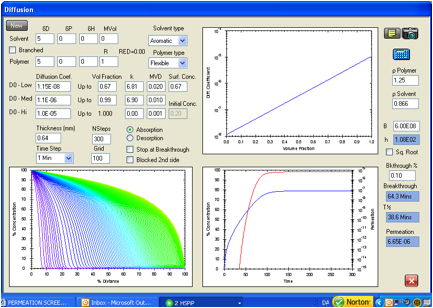
Figure 1‑2 HSPiP model for the permeation of toluene in the Ansell Edmont Nitrile glove type 37-165. The literature data indicate an equilibrium permeation rate of 6.68E-06 g/cm²/s versus 6.65E-06 g/cm²/s in this analysis. The literature indicates a breakthrough time of 61 minutes by an unspecified experimental technique while this calculation gives 64.3 minutes. The criterion here is when the concentration at side 2 reaches 0.1% of the surface concentration (saturated swelling amount) on the exposed side.

Dibutyl phthalate  permeation in Nitrile glove Ansell Edmont type 37-165

Figure 3 indicates what might be expected from a larger challenge chemical such as the plasticizer dibutyl phthalate. Here the D₀ is taken as 1E-09 cm²/s extending linearly as the logarithm of D to the pure liquid where the diffusion coefficient is taken as being similar to that for many viscous liquids at 1E-06 cm²/s. The surface concentration is based on an assumed degree of swelling of 500% that is typical for “good” solvents for this elastomer. The breakthrough time is 6.3 hours compared with the F/K data for the system which simply states >360 minutes. This shows that such low diffusion coefficients are not usually of greatest interest to protective clothing. To reduce costs there is room for adjusting other parameters such as film thickness, composition, crosslinking, etc. while still maintaining acceptable safety. What this calculation has shown is that D₀ is not larger than 1E-09 cm²/s, and probably is much lower depending on the actual breakthrough time.

 

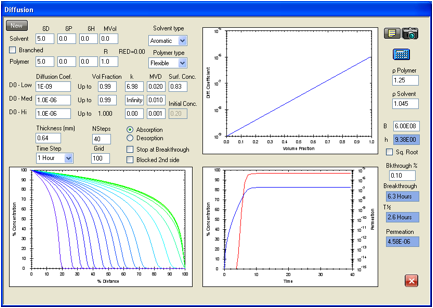
Figure 1‑3 HSPiP model for the permeation of dibutyl phthalate in the Ansell Edmont Nitrile glove type 37-165. The literature data indicate an equilibrium permeation rate of <1.5E-05 g/cm/s which is easily satisfied by the 4.58E-06 g/cm/s found here. The literature indicates a breakthrough time of >6 hours by an unspecified experimental technique while this calculation gives 6.3 hours. The criterion used here is when the concentration at side 2 reaches 0.1% of the surface concentration (saturation swelling amount) on the exposed side. The diffusion coefficients could be lower than those indicated in the figure.

Figure 3 also provides insight into what happens with a short term exposure for such large molecules. There is a possibility for considerable absorption at shorter times, which also strongly suggests that desorption of plasticizers into challenge liquids will also occur to a significant extent near the surface, even for shorter exposure times. The reason for this remark will become clear when we discuss the Butyl glove below. The first curve in the lower left hand figure for concentration versus distance is for an exposure time of about 12 minutes, where the uptake is 15% of the saturation value with a penetration depth at about 20% of the film thickness (0.64 mm).

The F/K data collection does list one Nitrile glove type, North LA.142G, where the breakthrough time for dibutyl phthalate is given as >960 minutes for a thickness of 0.33 mm. An analysis similar to the one above suggests the D₀ in this case is less than 4E-13 cm²/s for the same surface concentration. It is quite possible that this value is too low. The long breakthrough time with the thinner film could be caused by a lower surface concentration possibly supplemented by a stiffer glove material. Lowering the surface concentration to 0.6 volume fraction and use of a D₀ equal to 1E-10 cm²/s gives a breakthrough time of 18.3 hours, just exceeding the breakthrough time requirement.

 

Methanol permeation in Nitrile glove Ansell Edmont type 37-165

The permeation of methanol in the Ansel Edmont Nitrile glove type 37-165 is analyzed in Figure 4. The F/K data source gives a breakthrough time of 11 minutes with a permeation rate <9000 mg/m²/min, which converts to <1.5E-05 g/cm²/s. The equilibrium swelling (data, again, from Dr Lara) is 0.32 volume fraction which is taken as the surface concentration. The self-diffusion coefficient for methanol is close to 1.8E-05 cm²/s. Figure 4 shows a breakthrough time of 11.3 minutes and a permeation rate of 3.09E-06 g/cm/s. This permeation rate is far below the limit given above, and presumably is a good estimate of the actual rate. This is, again, an advantage of the mathematical modeling, because some permeation rate values may still be important, but may not be measurable. These can be reasonably estimated with limited knowledge of the system. D₀ is found as 2.4E-07 cm²/s, in agreement with expectations related to very small, linear molecules.

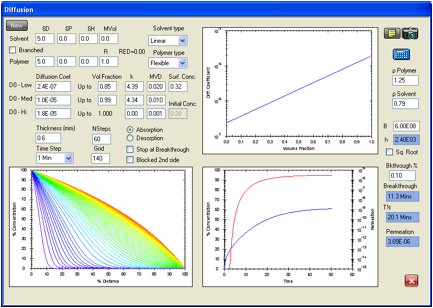
Figure 1‑4 HSPiP model for the permeation of methanol in the Ansell Edmont Nitrile glove type 37-165. The literature data indicate an equilibrium permeation rate of <1.5E-05 g/cm²/s which is in agreement with the 3.09E-06 g/cm²/s in this analysis.

The literature indicates a breakthrough time of 11 minutes by an unspecified experimental technique while this calculation gives 11.3 minutes. The criterion here is when the concentration at side 2 reaches 0.1% of the surface concentration on the exposed side.

 

Toluene permeation in Butyl rubber glove Best Company 878

Butyl rubber consists of about 98% isobutene and 2% isoprene with some variation in composition between different sources. It is widely used for chemical protective gloves because of excellent resistance to commonly used chemicals. These calculations used the data of Evans et.al.(Katherine M. Evans, Wumin Guo, and James Hardy, Modeling Solubility Parameters and Permeation Data of Organic Solvents Versus Butyl Gloves from Four Manufacturers, J. Appl. Poly. Sci., Vol. 109, 3867-3877 (2008)). This is a very complete study and again there is significant variation among the suppliers. We use their toluene data for the Best company type 878 glove in order to show the differences between Butyl rubber and the Nitrile glove studied above. The targets are a breakthrough time of 26.8 minutes (ASTM criterion) and a permeation rate of 1.29E-05 g/cm²/s. The equilibrium solubility is essentially the same as in the nitrile gloves at 0.865 volume fraction. Because of the almost identical solubility, it can immediately be seen that the diffusion coefficients will be higher for this Butyl glove than for the Nitrile glove discussed in the above. This is because the breakthrough time is shorter for a somewhat thicker film (0.75 mm versus 0.64mm).

A factor of some apparent importance for the performance of this glove type is that Evans et.al. found about 19 percent weight loss after careful removal of all solvent absorbed during the permeation testing. The glove contains about 19% plasticizing material. During a permeation test some of this plasticizing material will be partly removed from the exposed surface, thus reducing the inherent diffusion coefficient(s) attributable to the original material in this region.

The diffusion coefficients at concentrations just under the surface concentration were lowered in an attempt to simulate removal of plasticizer from the surface region of the glove. This was done by using a break in the diffusion coefficient profile at a concentration below the surface concentration. This lower slope at higher concentrations allows better fits of the experimental data than for the previously used straight line profiles, indirectly confirming the loss of some plasticizer.

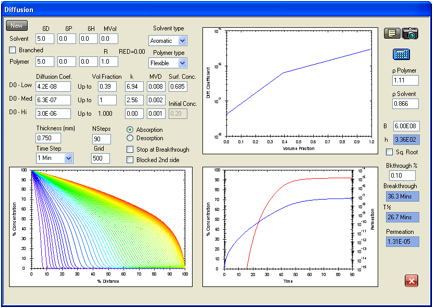
Figure 1‑5 Permeation of toluene in the Best company glove type 878. The break in the diffusion coefficient profile gives a better fit of the data, and could reflect migration of plasticizer from the glove to the toluene. The ASTM criterion give a breakthrough time of 26.7 minutes versus the target 26.8 minutes. The target permeation rate of 1.29E-05 g/cm²/s is well matched by the calculated permeation rate of 1.31E-05 g/cm²/s

Figures 6 and 7 repeat the examples reported in Figures 2 and 4, but with the ASTM criterion as a target for the breakthrough time. For comparison the ASTM breakthrough criterion would give breakthrough times for toluene in the Nitrile glove in Figure 2 equal to 56.8 minutes and for methanol in the Nitrile glove in Figure 4 equal to 5.7 minutes.

 

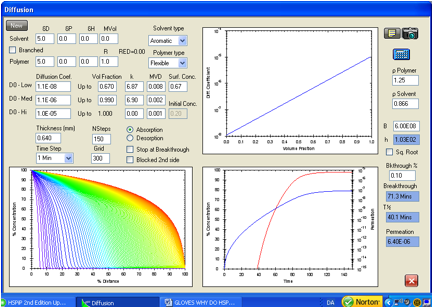
Figure 1‑6 Repeat of the permeation calculation for toluene in the Ansell Edmont Nitrile glove type 37-165. The ASTM criterion for breakthrough gives 60.7 minutes by interpolation of the red curve to a permeation rate of 1.67E-09 g/cm²/s. The target is 61 minutes. The diffusion coefficient profile is essentially unchanged from that used above in Figure 2. The equilibrium permeation rate is 6.4E-06 g/cm²/s. This is very close to the target value of 6.68E-06 g/cm²/s. Note that the grid line density is extended to 300.

 

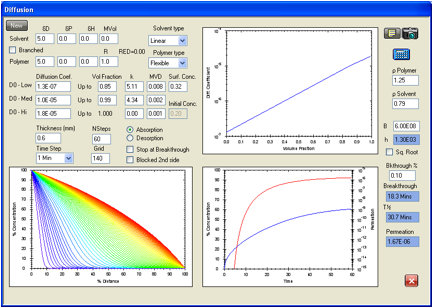
Figure 1‑7 Repeat of the permeation calculation for methanol in the Ansell Edmont Nitrile glove type 37-165. The ASTM criterion for breakthough times gives 11.3 minutes to compare with the 11 minutes given in the Forsberg/Kieth performance handbook. The permeation rate of 1.67E-06 g/cm²/s is much lower than the <1.5E-05 g/cm²/s required by the data. D₀ has been decreased from 2.4E-07 cm²/s to 1.3E-07 cm²/s to accommodate the change in the breakthrough criterion while maintaining the same equilibrium permeation rate.

 

Acetone permeation in Natural Rubber gloves

There are data in the F/K Chemical Protective Clothing Performance Index for the permeation of many different chemicals through natural rubber gloves, but many chemicals degrade the natural rubber. It should perhaps be noted again that there is wide variation in performance among the gloves. Solubility data provided by Dr. Lara have been used to try to select a system to study where the solubility is not too high. The glove type for which solubility data is available is Ansell 356, but this glove type is not included in the F/K source. This glove has a solubility of acetone equal to 0.162 volume fraction.

Figure 8 below matches the target breakthrough time (5 minutes) very well at 5.3 minutes with a permeation rate of 1.71E-06 g/cm²/s where the target is 1.84E-06 g/cm²/s. This is good agreement, and shows that reasonable estimates can be used to develop the diffusion coefficient profiles in natural rubber.

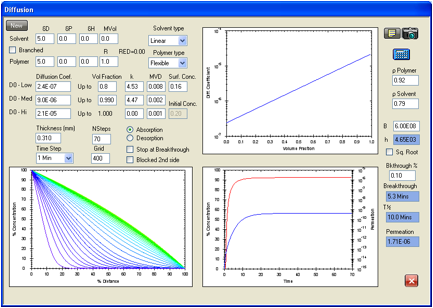
Figure 1‑8 Permeation of Acetone in natural rubber. F/K data used are for Ansell Edmont 46-320. The breakthrough time for this glove type in the F/K data is 5 minutes for a permeation rate of 1.837E-06 g/cm²/s.

Methanol permeation in Natural Rubber gloves

The F/K data source shows a wide variety of data for the permeation of methanol through different glove qualitites. Ansell Edmont glove 46-320 was selected for this study. The reported breakthrough time is 20 minutes and the permeation rate is 1.34E-07 g/cm²/s for a thickness of 0.31 mm. The results in Figure 9 for a surface concentration given by Dr Lara as 0.086 volume fraction are in excellent agreement with the literature data. The diffusion coefficient profile yielded an ASTM breakthrough time of 20.0 minutes. The calculated permeation rate is 1.32E-07 g/cm²/s. 

 

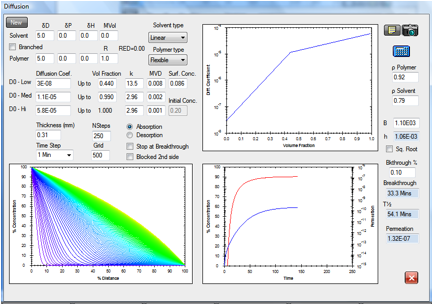
Figure 1‑9 Permeation of methanol in Natural Rubber. The given diffusion coefficient profile yielded an ASTM breakthrough time of 20 minutes versus the reported value of 20.0 minutes. The calculated permeation rate is 1.32E-07 g/cm²/s versus the reported value 1.34E-07 g/cm²/s.

It should be noted here that the methanol permeation data for some glove types could not be matched. An example of such a situation is Ansell Orange 208. The reported breakthrough time is 17 minutes, not far from that in the previous example, but the permeation rate is reported as 1.5E-09 g/cm²/s. This permeation rate is lower than the ASTM breakthrough criterion of 1.67E-09, and could simply not be matched by a reasonable diffusion coefficient profile. This reported permeation rate is 89 times lower than that reported for methanol in the natural rubber used in the previous example, and this for comparable breakthrough times. No explanation of this is obvious.

It is concluded, however, that permeation through natural rubber gloves can be modeled by the HSPiP software, with any exceptions to reasonable results requiring an explanation.

 

Methylene chloride permeation in Viton gloves

The data source for the following calculations for methylene chloride (Figure 10), chloroform (Figures 11a and 11b), and acetonitrile (Figure 12) in Viton is:

Katherine M. Evans and James K. Hardy, Predicting Solubility and Permeation Properties of Organic Solvents in Viton Glove Material Using Hansen’s Solubility Parameters, Journal of Applied Polymer Science, Vol. 93, 2688-2698 (2004). This is a very careful and thorough study providing the data needed.

 

The breakthrough time for methylene chloride in the given Viton glove material was 38.4 min with a steady state permeation rate of 1.15E-06 g/cm²/s. Figure 10 shows that these values can be duplicated with the diffusion coefficient profile given in the figure. The ASTM breakthrough time is calculated as 38.3 minutes with a permeation rate of 1.13E-06 g/cm²/s. 

 

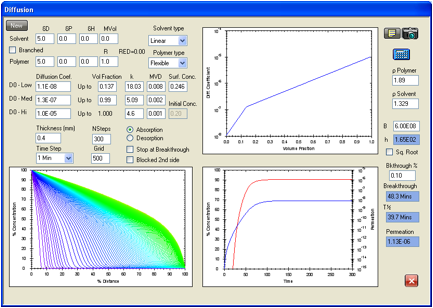
Figure 1‑10 Permeation of methylene chloride in Viton. The agreement is excellent with the reported breakthrough time of 38.4 minutes being matched with 38.3 minutes, and the reported steady state permeation rate of 1.15E-06 g/cm²/s was matched with a calculated 1.13E-06 g/cm²/s.

 

Chloroform permeation in Viton gloves

Figure 11 gives a diffusion coefficient profile for chloroform permeation in Viton. There is a calculated ASTM breakthrough time of 6.87 hours versus an experimental value of 6.90 hours and a steady state permeation rate of 6.18 g/cm²/s compared with the value from Evans and Hardy of 4.15 g/cm²/s. It has not been possible to find a set of parameters to better match both of these simultaneously. It is possible that a treatment similar to the one presented in the following for the permeation of acetonitrile could improve the agreement, but at the same time there is better agreement with another source of permeation data in this system also reported by Evans and Hardy as shown in Figure 12. In this second case the calculated value of the ASTM breakthrough time is 9.3 hours versus an experimental 9.5 hours. The calculated steady state permeation rate is 4.53E-08 g/cm²/s to be compared with an experimental value of 4.67E-08 g/cm²/s.

 

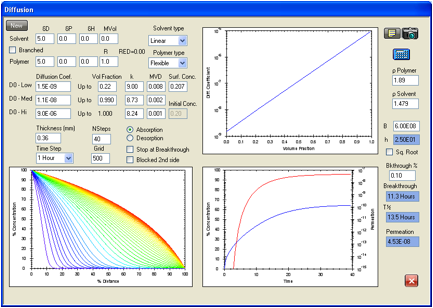
Figure 1‑11 Permeation data reported by Evans and Hardy for a previous study for chloroform in Viton. In this case the calculated value of the ASTM breakthrough time is 9.3 hours versus an experimental 9.5 hours. The calculated steady state permeation rate is 4.53E-08 g/cm²/s to be compared with an experimental value of 4.67E-08 g/cm²/s.

 

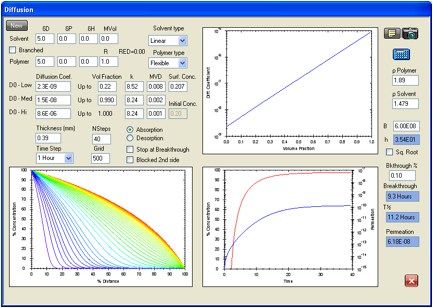
Figure 1‑12 There is a calculated ASTM breakthrough time of 6.87 hours versus an experimental value of 6.90 hours and a steady state permeation rate of 6.18 g/cm²/s compared with the value from Evans and Hardy of 4.15 g/cm²/s.

Acetonitrile permeation in Viton gloves

Evans and Hardy report an ASTM breakthrough time of 13.8 minutes and a steady state permeation rate of 1.95E-05 g/cm²/s for acetonitrile in Viton. Figure 13 gives the closest fit found for these values without trying to explore what a significant surface resistance might do. The data in Figure 13 reproduce the breakthrough time precisely at 13.8 minutes, but the calculated steady state permeation rate is 1.53E-05 g/cm²/s. While this might be satisfactory and probably within experimental error, an attempt was still made to explore the effect of a significant surface resistance.

 

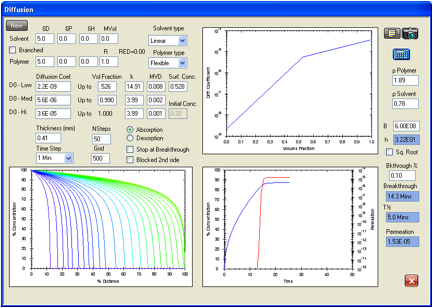
Figure 1‑13 Permeation of acetonitrile in Viton. Data of Evans and Hardy are reproduced exactly for the ASTM breakthrough time of 13.8 minutes but the steady state permeation rate is low at 1.53E-05 g/cm²/s compared with the experimental 1.97E-05 g/cm²/s.

 

Figure 14 shows the results of a significant surface effect. The change in the input values is a big reduction in the B value which in turn gives a limiting mass transfer coefficient, h of 1.27E-04. It is relevant to compare the estimated diffusion coefficients for acetonitrile (molar volume 52.6) with those of methylene chloride (molar volume 63.9). One would expect similar diffusion coefficients based on similarity of size (and shape) when comparing these two solvents. D₀ for methylene chloride is estimated in Figure 10 as 1.1E-08 cm²/s. D₀ for acetonitrile estimated with the inclusion of a significant surface effect is 9.5E-09 cm²/s , which is close to this, while without the significant surface effect, the D₀ is 2.2E-09 cm²/s . This expected similarity also speaks for the presence of a significant surface effect. The much larger equilibrium absorption of the acetonitrile is the main difference between these two solvents in the present context. This allows for very rapid diffusion within the Viton, and the supply through the surface cannot keep up with the removal from the surface.

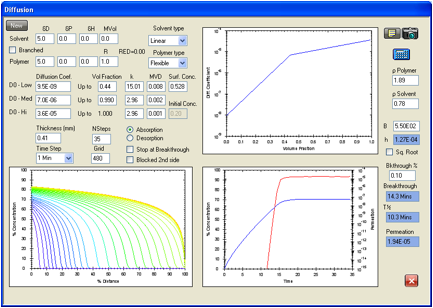
Figure 1‑14 Permeation of acetonitrile in Viton modeled with a significant surface resistance generated with a surface mass transfer coefficient, h, of 1.27E-04 cm/s. The ASTM breakthrough time here is 13.5 minutes compared with the experimental 13.8 minutes and the steady state permeation rate is 1.94E-05 g/cm²/s compared with 1.97E-05 g/cm²/s. The surface concentration at the steady state permeation condition is 0.832 times the solubility (0.528 volume fraction).

If one accepts this result, the effects of film thickness can be explored by maintaining the same h, and changing the thickness. The effect of putting on two gloves, for example can be estimated by entering a thickness of 0.82 mm and, neglecting any resistance between the gloves. Here one finds an ASTM breakthrough time of 39.1 minutes and a steady state permeation rate of 1.32E-05 g/cm²/s. The surface concentration is 0.882 times the solubility. The rule of thumb that the breakthrough time will be four times as large for a doubling of the film thickness would have indicated a breakthrough time of 4 times 13.5 which gives 54 minutes or 13.8 times 4 as 55.2 minutes. The reason for this difference is the surface condition has less effect on thicker films on a relative basis, and the higher concentrations in the film lead to higher diffusion coefficients. The gloves are not quite as safe as expected based on the rule of thumb.

A similar analysis of the steady state permeation rate would suggest that doubling the film thickness would cut the permeation rate in half. This is 0.98E-05 g/cm²/s compared with the 1.32E-05 g/cm²/s estimated by this calculation. Again the glove(s) are not as safe as predicted by the rule of thumb because there is more solvent in the glove, and the diffusion coefficients are higher than in the reference measurement.

These calculations should clearly be tested by experiment.

 

 

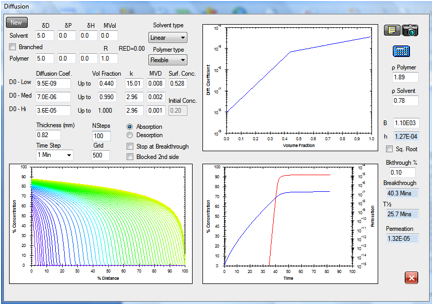
Figure 1‑15 Permeation of acetonitrile in Viton modeling the effect of wearing two gloves.

The ASTM breakthrough time is 39.1 minutes and the steady state permeation rate is 1.32E-05 g/cm²/s for a surface concentration that is 0.882 times the maximum amount that the Viton film can dissolve.

The time-lag

The time-lag calculation, now available in the Third Edition, was not used in any of the previous figures in the chapter. The values that would have been found are reported in the following table for permeation in Viton gloves only. The study by Evans and Hardy is the only source of the experimental information used for this purpose, and this is for Viton gloves only. The time-lag is the time value found by extrapolating the accumulated permeation rate back to zero amount permeated as seen in Figure 17-16.

Figure	Solvent	Experimental Time-lag	Calculated Time-Lag
17-10	Methylene chloride	55.7 min.	72.6 min.
17-11	Chloroform	677 min.	1194 min.
17-12	Chloroform	661.5 min.	984 min.
17-13	Acetonitrile	25.6 min.	15.1 min.
17-14	Acetonitrile	25.6 min.	16.1 min.
17-15	Acetonitrile	-	-
17-16	Acetonitrile	25.6 min.	25.2 min.

 

From the above table only marginal change can be seen comparing the time-lag of 15.1 minutes from Figure 17-13, where there is not significant entry surface resistance in the calculation, to the 16.1 minutes found in Figure 17-14, where there is. Both are still well below the experimental 25.6 minutes. The calculated and experimental steady state permeation rates and breakthrough times match well for the calculations in the latter figure, however. The time-lag data for the other figures is calculated as being much longer than measured. The reason for this is not known, but there is a strong suspicion that this is caused by surface resistance, perhaps mainly on the exit side of the samples in permeation cells as discussed in the following.

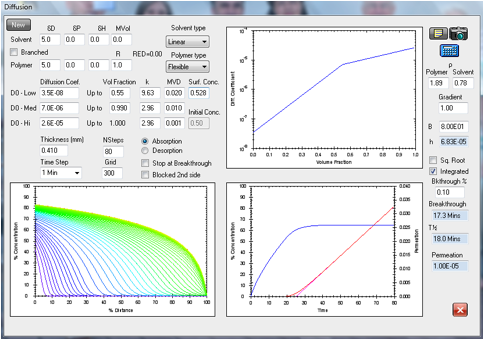
Figure 1‑16  Test of the lag-time calculation in the 3^rd Edition using the system acetonitrile in Viton as in the previous figures. The experimental time-lag is 25.6 minutes in excellent agreement with the calculated 25.2 minutes, and calculated breakthrough time of 13.5 minutes matches the experimental value of 13.5 minutes. However, the steady state permeation rates are not well matched with 1.00E-05 g/cm²/s calculated versus 1.95 g/cm²/s found experimentally.

Figure 17-16 gives data that match the lag-time and breakthrough time very well, including a significant surface resistance on the entry side, but the steady state permeation rate is much too slow. Matching the experimental and calculated permeation rates in Figure 17-16 would require a significantly higher surface concentration while keeping the same diffusion coefficient profile that gave the good matches in the time-lag and breakthrough time. This is not possible. Attempts to reconcile this in various ways did not lead to an improved result. It should be noted, however, that the there are only two relevant entries in the F/K database for acetonitrile in Viton (both for North F-091). The one lists degradation and the other a more rapid breakthrough (6 minutes) than in the example above, although the film thickness is smaller (0.26 mm). This leads one to suspect that the breakthrough and time lag data reported in Figure 17-16 are more reliable than are the steady state permeation data, and that some degradation in the Viton may be responsible for the higher experimental steady state permeation rate than is predicted by these calculations.

At this point in time there is too much variation in literature data and too many variables to properly assign accurate values to all of the relevant parameters, but each of the parameters discussed has, or easily can have significance, particularly for more rapid permeation in thinner samples.

Breakthrough times for low concentration exposures

It is possible to predict effects that are very difficult to measure when reliable diffusion coefficient profiles have been established. One of these is how quickly breakthrough occurs for a very limited exposure to a challenge chemical. This is not easily estimated from general permeation data which are typically measured at high concentrations with pure liquid exposure in permeation cells. The following tables report breakthrough times for low (constant) surface concentrations for the Nitrile glove type studied in the above using the diffusion coefficient profiles for toluene and methanol that were established in Figures 2 and 4. Like all numerical modelers there is some trade-off of accuracy (grid size) and speed so the values reported below are somewhat grid dependent. However it should also be noted that differences in breakthrough times for toluene with different types of Nitrile gloves far exceed any numerical uncertainties. For toluene the variation is from a low of about 4 minutes up to a high of 61 minutes. For methanol the variation is from a low of 7 minutes to a high of >480 minutes. One must be very careful with generalizations. The following is an indication of what is generally expected, but cannot be considered a complete analysis.

C1	Breakthrough time	Dmax/D0
0.00	-	1.00
0.01	496	1.04
0.02	486	1.13
0.05	452	1.39
0.10	402	2.0
0.67	64.3 (61)	86.9

 

Breakthrough times in minutes for toluene in the Nitrile glove Ansel Edmont type 37-165 for given

 

C1	Breakthrough time	Dmax/D0
0.00	-	1.00
0.01	21.3	1.04
0.02	21.3	1.08
0.05	20.3	1.25
0.10	19.3	1.54
0.32	11.3(11)	4.08

 

Breakthrough times in minutes for methanol in the Nitrile glove Ansel Edmont type 37-165 for given values of the surface concentration, C₁,  in volume fraction.

 

These data emphasize once more the importance of keeping diffusion coefficients low, one way or another, to keep breakthrough times long.

Practical implications

It’s a good idea to remind ourselves why we’ve gone to such lengths to analyze all that data. The reason is that it matters! The safety of real people with real chemicals depends on these analyses.

The problem is that there are many more chemicals than there are people to do the careful measurements of breakthrough times and permeation rates. We therefore need rational ways to arrive at the best choice of glove.

We’re already off to a good start. From the above analysis we can say that the majority of the D₀ values of interest to glove safety will lie between the limits of about 1E-09 cm²/s for larger molecules and about 1E-07 cm²/s for smaller molecules with an average near 1E-08 cm²/s. Figure 1 gives you an idea of how to estimate relative D₀ values if (as is usually the case) you don’t have the resources to measure them yourselves.

It is also clear that a greater HSP distance is required for safety when the molecules are smaller or more linear. Solvents with smaller molecules often appear as outliers in simple HSP correlations, getting through the glove more quickly than expected. Conversely experience has also shown that the phthalate plasticizers, for example, do not get through given glove types quickly, in spite of good matches in HSP with the glove materials. The reason for this is clearly portrayed above as a very low D₀.

For molecules beyond simple solvents and plasticizers, a method to improve the simplest HSP analyses in such situations has been given in Chapter 12. This uses the example of Neoprene gloves with a 1 hour breakthrough time. HSP can lead to reasonable predictions of breakthrough times for complex chemicals. If you have the luxury of more data then you can use the techniques described in this chapter to provide even better information.

Wearing two pairs of gloves, or a gloves of twice the thickness, gives four times the protection against diffusion and gives extra protection against accidental tears or punctures.

There will be times when simple estimates can lead you astray. As the acetonitrile/Viton example shows, without knowing that there is a strong surface resistance, the “twice the thickness gives four times the protection” guide leads to a false conclusion. However, most of us would not want to use gloves that so obviously loved to absorb so much solvent. Once again, a large HSP mismatch is a much better idea.

Because D₀ is usually lower in more rigid polymers than in more flexible polymers, the cautious user might like to go for a glove made from, say, polyethylene. But of course its very rigidity (lack of comfort) and the ease with which it is torn are often good reasons for not using it.

In summary, as in the previous chapter, the intelligent use of whatever data is to hand can lead to reasonable and defensible conclusions. In the absence of any other data then the best rule of safety is to maximize the HSP distance between the glove material and the challenge chemical with a glove material that is as flexible and comfortable as possible.

 

E-Book contents | HSP User's Forum