

| Home | 化学 | HSP | 情報化学+教育 | PirikaClub | Misc. |
| 化学トップ | 物性化学 | 高分子 | 化学工学 | その他 |
2005.1.14
Ab Initio計算は早いもので1日、遅いと1ヶ月かかる事もあります。平均すると3-4日と言ったところでしょうか? (Mac G4 1GHzくらいで。Windowsでは同じHzで1.5倍ぐらい早い感じがします。)これを早いと見るか遅いと見るかはいろいろでしょうがMOPACのPM3の活性化エネルギーをニューラルネットワークで推算したように、このB3LYPの計算結果を再現できるようなニューラルネットワークを構築してみます。それができれば瞬間で答えが出るはずです。
まず活性化エネルギーですが、遷移状態が求まったら計算結果の中の
| Zero-point correction= 0.147422 (Hartree/Particle) Thermal correction to Energy= 0.157256 Thermal correction to Enthalpy= 0.158200 Thermal correction to Gibbs Free Energy= 0.110709 Sum of electronic and zero-point Energies= -327.268759 Sum of electronic and thermal Energies= -327.258924 Sum of electronic and thermal Enthalpies= -327.257980 Sum of electronic and thermal Free Energies= -327.305471 E (Thermal) CV S KCAL/MOL CAL/MOL-KELVIN CAL/MOL-KELVIN TOTAL 98.679 33.773 99.954 ELECTRONIC 0.000 0.000 1.377 TRANSLATIONAL 0.889 2.981 39.950 ROTATIONAL 0.889 2.981 29.195 |
エンタルピーとエントロピーの値を抜き出します。原料のラジカルとモノマーからも同じように抜き出して反応の前後の差をとります。そして次のような表を作ります。
| name | dE | RaSOMO | RaLUMO | RaHCharge | MonHOMO | MonLUMO | MonTCharge |
| AA-AN | 6288.6127 | -10.118 | -0.814 | -0.1489 | -10.886 | -0.187 | -0.099 |
| AMD-AMD | 6731.0468 | -10.024 | -0.48 | -0.1804 | -10.925 | 0.143 | -0.0608 |
| AM-VC | 8296.1964 | -10.017 | -0.711 | -0.1578 | -9.837 | 0.704 | -0.1621 |
| AMD-AllC | 8110.4368 | -10.024 | -0.48 | -0.1804 | -10.269 | 0.621 | -0.1398 |
| AA-Vac | 6889.1934 | -10.118 | -0.814 | -0.1489 | -10.083 | 0.687 | -0.2102 |
| VDC-St | 6283.5922 | -8.803 | 0.16 | -0.3909 | -9.13 | -0.122 | -0.1581 |
| AA-Acro | 4353.8267 | -10.118 | -0.814 | -0.1489 | -10.681 | -0.098 | -0.0493 |
こうしたものをB3LYP/6-31G**で遷移状態の求まっている247組分用意します。最初のカラムは名称、次はエンタルピーの変化量(活性化エネルギー)です。そしてその後の6つのカラムは活性化エネルギーを説明する説明因子で、これが味噌なのですがここでの値にMOPAC PM3の時と同じようにMOPACで計算したラジカルとモノマーの物性値が入っています。つまりMOPACの計算値からB3LYPの計算値を推算するのです。新しいモノマー、新しいラジカルの遷移状態への活性化エネルギーを予測したかったらMOPACで原料を計算するだけでB3LYPレベルの予測ができるようにする。のが今回の目的です。
入力する項目はラジカルのSOMO、LUMOとラジカルヘッドの電荷、モノマーのHOMO、LUMO、モノマーテイルの電荷の6種類、MOPACでやったときと全く同じです。中間層の数やバイアスも前と同じで学習させます。
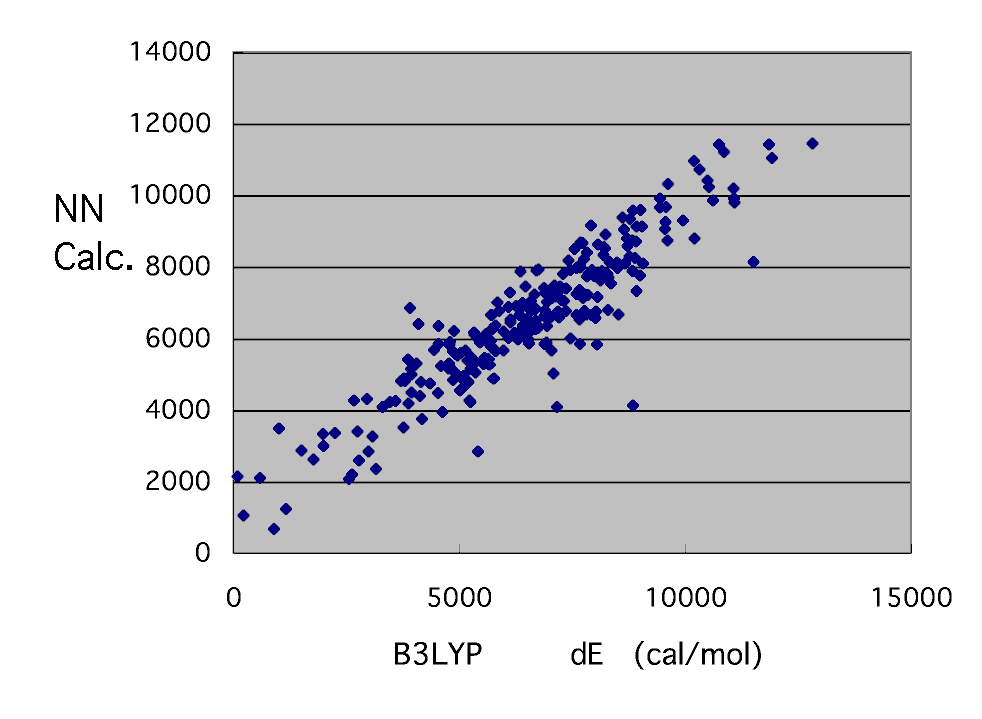
明らかにおかしな点がいくつかありますがMOPACと違って簡単に再計算して修正する訳にはいきません。さしあたって取り除いておいて後でゆっくり何故おかしいのかチェックする事にします。系統だっておかしなものは無いようです。
そして最終的には
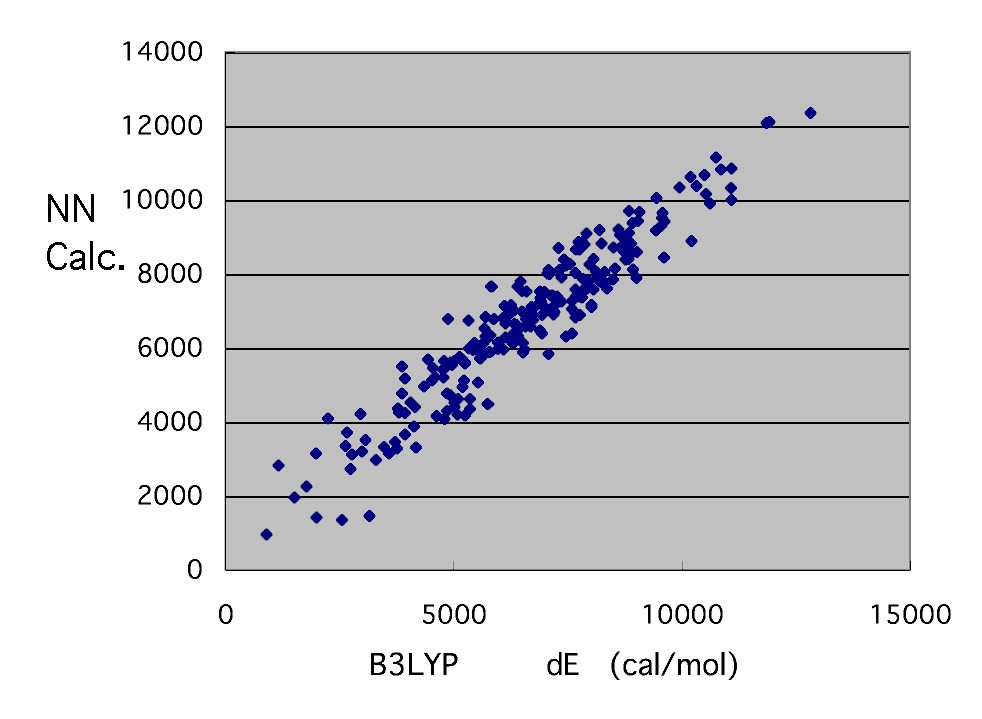
こんな結果が得られました。dEが小さな2-4kcal/molあたりでばらつきが大きいですが結構良好にB3LYPの結果を再現できていると言えます。
次には頻度因子Aの推算です。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。